练习册系列答案
相关题目
如图,自行车每节链条的长度为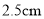 ,交叉重叠部分的圆的直径为
,交叉重叠部分的圆的直径为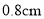 .
.
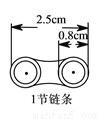


( )观察图形,填写下表:
)观察图形,填写下表:
链条的节数/节 |
|
|
|
|
链条的长度/ |
|
(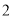 )如果
)如果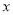 节链条的长度是
节链条的长度是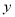 ,那么
,那么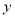 与
与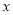 之间的关系式是什么?
之间的关系式是什么?
(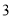 )如果一辆某种型号自行车的链条(安装前)由
)如果一辆某种型号自行车的链条(安装前)由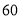 节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?
节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?
如图,自行车每节链条的长度为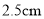 ,交叉重叠部分的圆的直径为
,交叉重叠部分的圆的直径为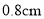 .
.
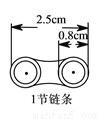


( )观察图形,填写下表:
)观察图形,填写下表:
链条的节数/节 |
|
|
|
|
链条的长度/ |
|
( )如果
)如果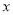 节链条的长度是
节链条的长度是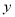 ,那么
,那么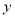 与
与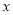 之间的关系式是什么?
之间的关系式是什么?
(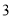 )如果一辆某种型号自行车的链条(安装前)由
)如果一辆某种型号自行车的链条(安装前)由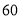 节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?
节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?