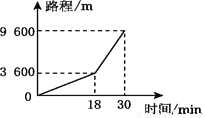
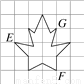
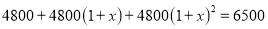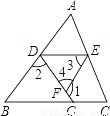题目内容
正方形OABC的边长为2,其中OA、OC分别在x轴和y轴上,如图①所示,直线l经过A、C两点.
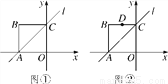
(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标;
(2)如图②,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点.
①请求出|BE+DE|的最小值和此时点E的坐标;
②若将点D沿x轴翻折到x轴下方,直接写出|BE-DE|的最大值,并写出此时点E的坐标.
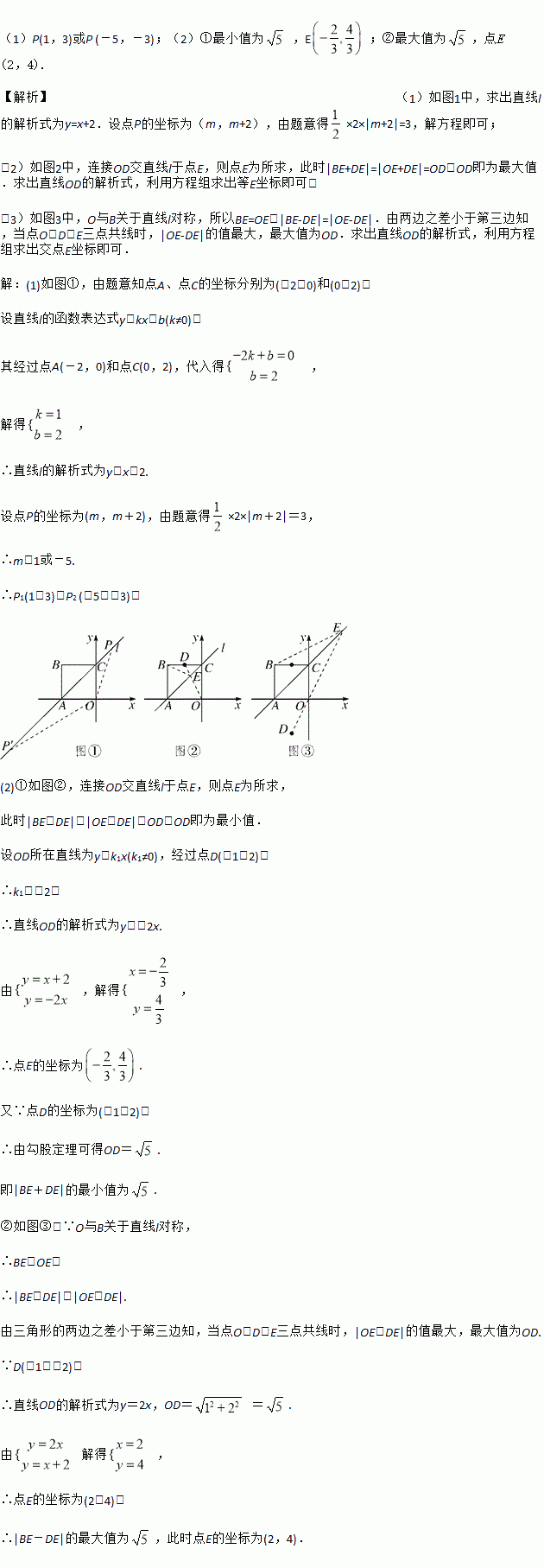
(1)P(1,3)或P (-5,-3);(2)①最小值为 ,E ;②最大值为,点E (2,4). 【解析】(1)如图1中,求出直线l的解析式为y=x+2.设点P的坐标为(m,m+2),由题意得×2×|m+2|=3,解方程即可; (2)如图2中,连接OD交直线l于点E,则点E为所求,此时|BE+DE|=|OE+DE|=OD,OD即为最大值.求出直线OD的解析式,利用方程组求出等E坐标即可...
练习册系列答案
相关题目

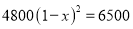 B.
B. 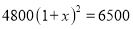
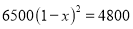 D.
D.