题目内容
7.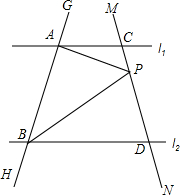 已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合).
已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合).(1)如图,如果点P在线段CD上时,试找出∠PAC、∠PBD、∠APB之间的关系并说出理由.
(2)如果点P不在线段CD上时,试探究∠PAC、∠PBD、∠APB之间的关系(只要写出结论即可,不要证明).
分析 (1)过P作PE∥AC,根据平行线的性质可得∠CAP=∠1,∠PBD=∠2,进而可得∠APB=∠CAP+∠PBD;
(2)根据题意作图,由平行线与外角的性质即可求得答案.
解答 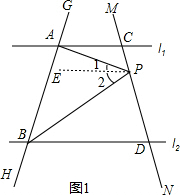 解:(1)如图1,过P作PE∥AC,
解:(1)如图1,过P作PE∥AC,
∵l1∥l2,
∴AC∥EP∥DB,
∴∠CAP=∠1,∠PBD=∠2,
∴∠APB=∠CAP+∠PBD;
(2)如图2,若点P在AC下方,
设PA交BD于点E,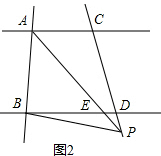 ∵AC∥BD,
∵AC∥BD,
∴∠PAC=∠PED,
∵∠PED=∠PBD+∠APB,
∴∠APB=∠PBD-∠PAC,
若点P在AC上方,则∠APB=∠PBD+∠PAC.
点评 此题主要考查了平行线的性质,关键是掌握两直线平行,内错角相等.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

 如图,OP是∠AOB的平分线,点C在射线OA上,点D在射线OB上.若AC=BD,则S△ACP=S△BDP(填“>”“<”或“=”).
如图,OP是∠AOB的平分线,点C在射线OA上,点D在射线OB上.若AC=BD,则S△ACP=S△BDP(填“>”“<”或“=”).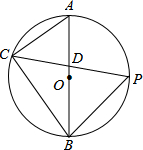 如图,AB是⊙O的直径,点P是$\widehat{AB}$的中点.
如图,AB是⊙O的直径,点P是$\widehat{AB}$的中点. 在某节习题课上.老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.
在某节习题课上.老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.