题目内容
15. 如图,OP是∠AOB的平分线,点C在射线OA上,点D在射线OB上.若AC=BD,则S△ACP=S△BDP(填“>”“<”或“=”).
如图,OP是∠AOB的平分线,点C在射线OA上,点D在射线OB上.若AC=BD,则S△ACP=S△BDP(填“>”“<”或“=”).
分析 如图,作辅助线;首先运用角平分线的性质证明PM=PN,借助三角形的面积公式即可解决问题.
解答  解:如图,过点P作PM⊥OA、PN⊥OB;
解:如图,过点P作PM⊥OA、PN⊥OB;
∵OP是∠AOB的平分线,
∴PM=PN;而AC=BD,
∴$\frac{1}{2}AC•PM=\frac{1}{2}BD•PN$,
即S△ACP=S△BDP.
故答案为=.
点评 该题主要考查了角平分线的性质、三角形的面积公式等几何知识点及其应用问题;解题的关键是作辅助线,构造三角形的高线.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
10. 如图,数轴上点A表示数a,点B表示数b,则下列结论正确的是( )
如图,数轴上点A表示数a,点B表示数b,则下列结论正确的是( )
 如图,数轴上点A表示数a,点B表示数b,则下列结论正确的是( )
如图,数轴上点A表示数a,点B表示数b,则下列结论正确的是( )| A. | ab<0 | B. | |a|<|b| | C. | b-a<0 | D. | b-a>0 |
20. 观察图1,若天平保持平衡,在图2天平的右盘中需放入( )个○才能使其平衡.
观察图1,若天平保持平衡,在图2天平的右盘中需放入( )个○才能使其平衡.
 观察图1,若天平保持平衡,在图2天平的右盘中需放入( )个○才能使其平衡.
观察图1,若天平保持平衡,在图2天平的右盘中需放入( )个○才能使其平衡.| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
 如图,是一个数值转换机的示意图,若输入m的值为1,n的是为2014,则输出结果y为2014.
如图,是一个数值转换机的示意图,若输入m的值为1,n的是为2014,则输出结果y为2014.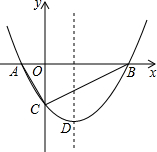 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0). 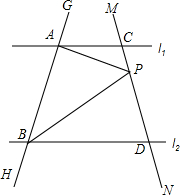 已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合).
已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合).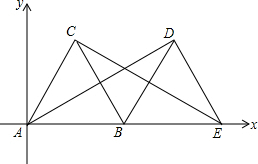 在平面直角坐标系中,如图所示,△ABC是边长为2的等边三角形,将△ABC绕着点B按顺时针方向旋转得到△EDB,使得点E落在x轴的正半轴上,连结CE、AD、
在平面直角坐标系中,如图所示,△ABC是边长为2的等边三角形,将△ABC绕着点B按顺时针方向旋转得到△EDB,使得点E落在x轴的正半轴上,连结CE、AD、