题目内容
19. 在某节习题课上.老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.
在某节习题课上.老师在黑板上写下了关于x的二次函数y=kx2+(k+1)x+2-4k.(1)某两位同学经过思考,对上述的二次函数进行了如下的总结:
①该二次函数的图象经过点(1,3);
②当k<0时,该二次函数的图象与y轴的正半轴有交点;
请你判断上面两条结论是真命题还是假命题,并说明理由;
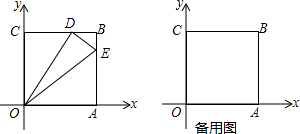
(2)若二次函数y=kx2+(k+1)x+2-4k的图象如图所示,该函数图象经过点B(-3,1),且与y轴交于点A,与x轴的负半轴交于点C,D为图象的顶点.
①求∠BAD的度数;
②点M在第三象限,且点M在二次函数图象上,连接OM,若∠ABD=∠MOC,求点M的横坐标.
分析 (1)①将(1,3)点代入函数,解出k的值即可作出判断;
②根据当k<0时,2-4k>0,即可判断;
(2)①将点B(-3,1)代入y=kx2+(k+1)x+2-4k,即可得出k的值,从而得出二次函数的解析式,即可得出点A、C、D的坐标,求得AB,AD,BD的长,再根据勾股定理的逆定理即可得出∠BAD的度数;
②设点M的坐标(xM,yM),根据∠ABD=∠MOC,即可得出tan∠ABD的值,从而得出点M的横坐标.
解答 解:(1)①假命题;将(1,3)代入可得:2k-(4k+1)-k+1=3,
解得:k=0.所以是假命题;
②是真命题,
理由:∵二次函数y=kx2+(k+1)x+2-4k的图象与y轴的交点为(0,2-4k),
当k<0,时,2-4k>0,
∴二次函数的图象与y轴的正半轴有交点;
(2)由二次函数y=kx2+(k+1)x+2-4k可知A(0,2-4k),D(-$\frac{k+1}{2k}$,$\frac{4k(2-4k)-(k+1)^{2}}{4k}$),
∵B(-3,1)在二次函数y=kx2+(k+1)x+2-4k的图象上,
∴9k-3(1-4k)+2-4k=1,
解得k=1,
∴抛物线的解析式为y=x2+2x-2,
∴A(0,-2),D(-1,-3)
∴AB=3$\sqrt{2}$,AD=$\sqrt{2}$,BD=2$\sqrt{5}$,
∵(3$\sqrt{2}$)2+$\sqrt{2}$2=(2$\sqrt{5}$)2,
∴AB2+AD2=BD2,
∴△ABD为Rt△,
∴∠BAD=90°;
②设点M的坐标(xM,yM),
∵∠ABD=∠MOC,
∴tan∠ABD=tan∠MOC,
∵tan∠ABD=$\frac{AD}{AB}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$,
∴tan∠MOC=$\frac{|yM|}{|xM|}$=$\frac{-{y}_{M}}{-{x}_{M}}$=$\frac{1}{3}$,
∴xM=3yM,
∴yM=$\frac{1}{3}$xM,
∵点M在二次函数图象上,
∴$\frac{1}{3}$x=x2+2x-2,
解得x=$\frac{-5±\sqrt{97}}{6}$,
∵点M在第三象限,
∴x<0,
∴x=$\frac{-5-\sqrt{97}}{6}$,
∴点M的横坐标$\frac{-5-\sqrt{97}}{6}$.
点评 本题考查了二次函数的综合题,还考查了点与函数的关系,待定系数法求二次函数的解析式以及三角函数、勾股定理的逆定理等知识.此题综合性较强,难度较大,解题的关键是方程思想与数形结合思想的应用.

 阅读快车系列答案
阅读快车系列答案 如图,数轴上点A表示数a,点B表示数b,则下列结论正确的是( )
如图,数轴上点A表示数a,点B表示数b,则下列结论正确的是( )| A. | ab<0 | B. | |a|<|b| | C. | b-a<0 | D. | b-a>0 |
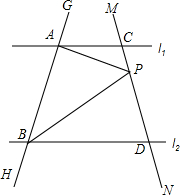 已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合).
已知直线l1∥l2,直线GH分别交l1、l2于A、B两点,直线MN分别交l1、l2于C、D两点,点P在直线MN上(点P和C、D不重合). 如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则圆弧AOB的长为$\frac{4}{3}$π.
如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则圆弧AOB的长为$\frac{4}{3}$π.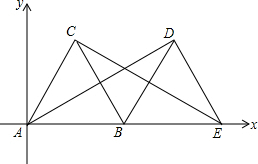 在平面直角坐标系中,如图所示,△ABC是边长为2的等边三角形,将△ABC绕着点B按顺时针方向旋转得到△EDB,使得点E落在x轴的正半轴上,连结CE、AD、
在平面直角坐标系中,如图所示,△ABC是边长为2的等边三角形,将△ABC绕着点B按顺时针方向旋转得到△EDB,使得点E落在x轴的正半轴上,连结CE、AD、