题目内容
有若干块长方形和正方形纸片如图所示,用若干块这样的硬纸片拼成一个新的长方形.
(1)用两种不同方法计算图(2)中长方形的面积,由此可得出一个等式 .
(2)有若干块如图(3)所示的长方形和正方形硬纸片
①请你用拼图方法推出一个完全平方公式,画出你的拼图.
②试借助拼图的方法,把二次三项式a2+4ab+3b2因式分解;画出拼图,并写出因式分解的结果.

(1)用两种不同方法计算图(2)中长方形的面积,由此可得出一个等式
(2)有若干块如图(3)所示的长方形和正方形硬纸片
①请你用拼图方法推出一个完全平方公式,画出你的拼图.
②试借助拼图的方法,把二次三项式a2+4ab+3b2因式分解;画出拼图,并写出因式分解的结果.
考点:因式分解的应用,完全平方公式的几何背景
专题:
分析:(1)要能根据所给拼图运用不同的计算面积的方法,来推导公式;
(2)要能根据等式画出合适的拼图.
(2)要能根据等式画出合适的拼图.
解答:解:(1)a2+2a+1=(a+1)2;
(2)①如图,

可推导出(a+b)2=a2+2ab+b2;
②如图,

所以a2+4ab+3b2=(a+b)(a+3b).
(2)①如图,

可推导出(a+b)2=a2+2ab+b2;
②如图,

所以a2+4ab+3b2=(a+b)(a+3b).
点评:本题考查运用正方形或长方形的面积计算推导相关的一些等式;运用图形的面积计算的不同方法得到多项式的因式分解.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
若不等式-ax>1的解集是x<-
,则( )
| 1 |
| a |
| A、a≥0 | B、a≤0 |
| C、a>0 | D、a<0 |
 如图,把一块直角形的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2是( )
如图,把一块直角形的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2是( )| A、65° | B、55° |
| C、60° | D、35° |
已知单项式-2a2m+3b5与3a5bm-2n的和是单项式,则(m+n)2013=( )
| A、1 | B、-1 | C、0 | D、0或1 |
某班同学毕业时将自己的照片向全班其他同学各送一张表示留念,全班共送2450张照片,如果全班有x名同学,根据题意,列出方程为( )
| A、x(x+1)=2450 |
| B、x(x-1)=2450×2 |
| C、x(x-1)=2450 |
| D、2x(x+1)=2450 |
 如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,求∠P的度数.
如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,求∠P的度数.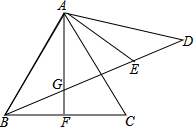 如图,△ABC是等边三角形,F是BC中点,G是AF上任意的一点,D在BG延长线上,且AD=AC,AE平分∠CAD交BD于E.
如图,△ABC是等边三角形,F是BC中点,G是AF上任意的一点,D在BG延长线上,且AD=AC,AE平分∠CAD交BD于E. 已知,如图AD是△ABC的角平分线,DE∥CA交AB于点E,DF∥BA交AC于点F.试问∠1=∠2吗?为什么?
已知,如图AD是△ABC的角平分线,DE∥CA交AB于点E,DF∥BA交AC于点F.试问∠1=∠2吗?为什么?