题目内容

5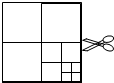．如图，将一张正方形纸片剪成四个小正方形，得到4个小正方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个小正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个小正方形，称为第三次操作；…；根据以上操作，若操作670次，得到小正方形的个数是（　　）
A．2009B．2010C．2011D．2012

分析 根据题意可以发现：每一次剪的时候，都是把上一次的图形中的一个进行剪．所以在4的基础上，依次多3个，继而解答各题即可．

解答 解：根据题意可知：后一个图形中的个数总比前一个图形中的个数多3个，
即剪第1次时，可剪出4个正方形；
剪第2次时，可剪出7个正方形；
剪第3次时，可剪出10个正方形；
剪第4次时，可剪出13个正方形；
…
剪n次时，共剪出小正方形的个数为：4+3（n-1）=3n+1．
当n=670时，正方形的个数为3×670+1=2011，
故选C．

点评 本题考查剪纸问题，同时考查规律型中的图形变化问题，同时考查学生观察、分析、归纳和应用规律的能力．

练习册系列答案
相关题目
15．梯形中位线长6cm，下底长8cm，则上底的长为4cm．
16．计算题
（1）（3$\sqrt{2}$-2$\sqrt{3}$）2-（3$\sqrt{2}$+2$\sqrt{3}$）2          
（2）$\sqrt{75}$×$\sqrt{50}$$÷\sqrt{6}$
（3）2$\sqrt{12}$+$\sqrt{27}$                   
（4）$\sqrt{48}$-9$\sqrt{\frac{1}{3}}$+3$\sqrt{12}$
（5）$\frac{\sqrt{72}-\sqrt{24}}{\sqrt{8}}$-（2+$\sqrt{3}$）2          
（6）4$\sqrt{\frac{1}{2}}$+3$\sqrt{\frac{1}{3}}$-$\sqrt{8}$．
13．我市民营经济持续发展，2013年城镇民营企业就业人数突破20万．为了解城镇民营企业员工每月的收入状况，统计局对全市城镇民营企业员工2013年月平均收入随机抽样调查，将抽样的数据按“2000元以内”、“2000元～4000元”、“4000元～6000元”和“6000元以上”分为四组，进行整理，分别用A，B，C，D表示，得到下列两幅不完整的统计图．

由图中所给出的信息解答下列问题：
（1）本次抽样调查的员工有500人，在扇形统计图中x的值为14，表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是21.6°；
（2）将不完整的条形图补充完整，并估计我市2013年城镇民营企业20万员工中，每月的收入在“2000元～4000元”的约多少人？
（3）统计局根据抽样数据计算得到，2013年我市城镇民营企业员工月平均收入为4872元，请你结合上述统计的数据，谈一谈用平均数反映月收入情况是否合理？
20．如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第6个图形需要黑色棋子的个数是（　　）
A．36B．40C．48D．50
10．先化简，再求值：2a2-[$\frac{1}{2}$（ab-4a2）-7ab]-$\frac{1}{2}$ab，其中a，b满足|a+$\frac{1}{2}$|+（b-3）2=0．
17．已知a2+bc=6，b2-2bc=-7．则5a2+4b2-3bc的值是（　　）
A．3B．2C．1D．0
14．已知等边三角形的边长为a，用a表示这个三角形的周长是3a．
15．先化简，后求值：2（x2y+xy）-3（x2y-xy）-x2y，其中x=1，y=-1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网