题目内容
9.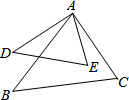 如图,若∠B=∠D,AD=4,DE=5,AB=6,BC=7.5,求证:∠DAB=∠CAE.
如图,若∠B=∠D,AD=4,DE=5,AB=6,BC=7.5,求证:∠DAB=∠CAE.
分析 根据相似三角形的判定与性质,可得∠DAE与∠BAC的关系,根据等式的性质,可得答案.
解答 证明:∵∠D=∠B,且$\frac{AD}{AB}$=$\frac{DE}{BC}$,
∴△ADE∽△ABC,
∴∠DAE=∠BAC.
∵∠DAE-∠BAE=∠BAC-∠BAE,
∴∠DAB=∠CAE.
点评 本题考查了相似三角形的判定与性质,利用了相似三角形的判定:两边对应成比例且夹角相等的两个三角形相似,相似三角形的对应角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.准备两组相同的牌,每组3张,分别是1、2、3,两张牌的牌面数之和等于5的频数是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\frac{1}{4}$ |
18.10月l2日,“重庆南开(融侨)中学第三届校史知识竞赛”在多功能厅举行,共24个班级参加比赛,其比赛成绩如下表所示;
则这24个班级比赛成绩的众数为90分.
| 成绩(分) | 80 | 90 | 100 | 120 | 150 | 170 |
| 班级数目(个) | 2 | 6 | 4 | 5 | 4 | 3 |
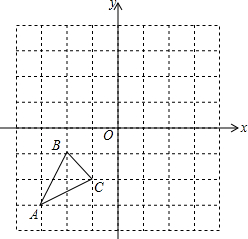 如图,在单位长度为1的方格中,若以点O为坐标原点建立平面直角坐标系,A(-3,-3),B(-2,-1),C(-1,-2).
如图,在单位长度为1的方格中,若以点O为坐标原点建立平面直角坐标系,A(-3,-3),B(-2,-1),C(-1,-2).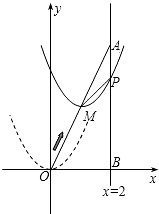 如图,在平面直角坐标系中,已知A点坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知A点坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.