题目内容
4.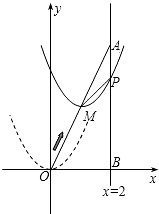 如图,在平面直角坐标系中,已知A点坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知A点坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.(1)求线段OA所在直线的函数解析式;
(2)设抛物线顶点M的横坐标为m,
①用m的代数式表示点P的坐标;
②当m为何值时,线段PB最短,最短是多少?
分析 (1)根据A点的坐标,用待定系数法即可求出直线OA的解析式.
(2)①由于M点在直线OA上,可根据直线OA的解析式来表示出M点的坐标,因为M点是平移后抛物线的顶点,因此可用顶点式二次函数通式来设出这个二次函数的解析式,P的横坐标为2,将其代入抛物线的解析式中即可得出P点的坐标.
②PB的长,实际就是P点的纵坐标,因此可根据其纵坐标的表达式来求出PB最短时,对应的m的值.
解答 解:(1)设OA所在直线的函数解析式为y=kx,
∵A(2,4),
∴2k=4,
∴k=2,
∴OA所在直线的函数解析式为y=2x.
(2)①∵顶点M的横坐标为m,且在线段OA上移动,
∴y=2m(0≤m≤2).
∴顶点M的坐标为(m,2m).
∴抛物线函数解析式为y=(x-m)2+2m.
∴当x=2时,y=(2-m)2+2m=m2-2m+4(0≤m≤2).
∴点P的坐标是(2,m2-2m+4).
②∵PB=m2-2m+4=(m-1)2+3,
又∵0≤m≤2,
∴当m=1时,PB最短是3.
点评 本题考查了二次函数综合题,涉及一次函数解析式的确定、二次函数图象的平移、函数图象的交点等知识点,同时考查了学生数形结合的数学思想方法.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
16.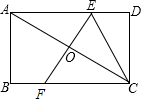 如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F,连接CE,则CE的长( )
如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F,连接CE,则CE的长( )
 如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F,连接CE,则CE的长( )
如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F,连接CE,则CE的长( )| A. | $\frac{9}{4}$ | B. | $\frac{11}{5}$ | C. | $\frac{15}{7}$ | D. | $\frac{13}{6}$ |
13.下列欧洲足球俱乐部标志中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.下列计算正确的是( )
| A. | a•a2=a2 | B. | (a2)2=a4 | C. | 3a+2a=5a2 | D. | (a2b)3=a2•b3 |
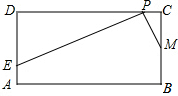 已知:在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C、D 两点).连接PM.过点P作PM的垂线与射线DA相交于点E(如图),设CP=x,DE=y
已知:在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C、D 两点).连接PM.过点P作PM的垂线与射线DA相交于点E(如图),设CP=x,DE=y 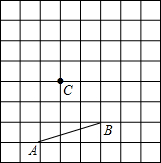 在如图所示方格纸中,按下述要求画图并回答:
在如图所示方格纸中,按下述要求画图并回答: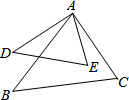 如图,若∠B=∠D,AD=4,DE=5,AB=6,BC=7.5,求证:∠DAB=∠CAE.
如图,若∠B=∠D,AD=4,DE=5,AB=6,BC=7.5,求证:∠DAB=∠CAE.