题目内容
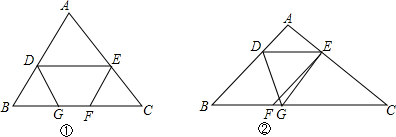
19.如图所示,在△ABC中,G为BC上一动点,∠C=45°,∠DBF=∠DEF,∠BDG=∠BGD,DG平分∠BDE.(1)如图①,当G点在BF上时,求证:BD∥EF;
(2)如图②,当G在CG上时,连接GE,若∠DEG=3∠FEG,∠DGE=60°,求线段GE与AC的位置关系,并证明.
分析 (1)求出∠EDG=∠BGD,根据平行线的判定得出DE∥BC,根据平行线的性质得出∠B+∠BDE=180°,求出∠DEF+∠BDE=180°,根据平行线的判定得出即可;
(2)设∠FEG=x°,∠DEG=3x°,∠DEF=2x°=∠DBG,根据平行线的性质求出∠BDE=180°-2x°,根据等腰三角形的性质和三角形的内角和定理求出∠BDG=∠EDG=90°-x°,根据平行线的性质求出90-x+60+3x=180,求出x,即可求出答案.
解答 (1)证明:∵DG平分∠BDE,
∴∠BDG=∠EDG,
∵∠BDG=∠BGD,
∴∠EDG=∠BGD,
∴DE∥BC,
∴∠B+∠BDE=180°,
∵∠DBF=∠DEF,
∴∠DEF+∠BDE=180°,
∴BD∥EF;
(2)GE⊥AC,
证明:∵∠DEG=3∠FEG,设∠FEG=x°,
∴∠DEG=3x°,∠DEF=2x°=∠DBG,
∵BD∥EF,
∴∠BDE+∠DEF=180°,
∴∠BDE=180°-2x°,
由(1)可知∠BDG=∠EDG=∠BGD=$\frac{1}{2}$(180°-∠DBG)=90°-x°,
∵DE∥BG,
∴∠DEG+∠BGE=180°,
又∵∠DGE=60°,
即90-x+60+3x=180,
∴∠FEG=x=15°,∠DEG=45°,
∵DE∥BC,
∴∠C=∠AED=45°,
∴∠AEG=90°,
∴GE⊥AC.
点评 本题考查了平行线的性质和判定,三角形内角和定理,等腰三角形的性质的应用,能综合运用平行线的性质和判定定理进行推理是解此题的关键,题目综合性比较强,难度偏大.

练习册系列答案
相关题目
7.下列命题中,假命题是( )
| A. | 长度相等的弧是等弧 | |
| B. | 等弧必须是同圆或等圆中的弧,否则不能互相重合 | |
| C. | 度数相等的弧不一定是等弧 | |
| D. | 等弧的度数相等 |
14.下列计算正确的是( )
| A. | a•a2=a2 | B. | (a2)2=a4 | C. | 3a+2a=5a2 | D. | (a2b)3=a2•b3 |
8.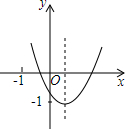 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )
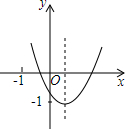 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )| A. | a<0 | B. | 2a+3b=0 | C. | a-b+c<0 | D. | c<-1 |
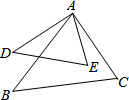 如图,若∠B=∠D,AD=4,DE=5,AB=6,BC=7.5,求证:∠DAB=∠CAE.
如图,若∠B=∠D,AD=4,DE=5,AB=6,BC=7.5,求证:∠DAB=∠CAE.
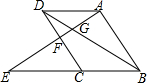 如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3.
如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3.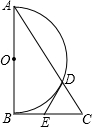 如图,在Rt△ABC中,∠ACB=90°,以AB为直径作半圆O交AC于点D,点E为BC的中点,连接DE.
如图,在Rt△ABC中,∠ACB=90°,以AB为直径作半圆O交AC于点D,点E为BC的中点,连接DE.