题目内容
19.(1)问题发现如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
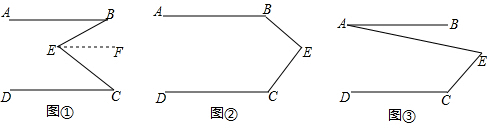
请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC(平行于同一直线的两直线平行)
∴∠C=∠CEF.(两直线平行,内错角相等)
∵EF∥AB,∴∠B=∠BEF(同理),
∴∠B+∠C=∠BEF+∠CEF(等量代换)
即∠B+∠C=∠BEC.
(2)拓展探究
如果点E运动到图②所示的位置,其他条件不变,求证:∠B+∠C=360°-∠BEC.
(3)解决问题
如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A=20°.(之间写出结论,不用写计算过程)
分析 (1)过点E作EF∥AB,根据平行线的判定得出AB∥CD∥EF,根据平行线的性质得出即可;
(2)过点E作EF∥AB,根据平行线的判定得出AB∥CD∥EF,根据平行线的性质得出即可;
(3)过点E作EF∥AB,根据平行线的判定得出AB∥CD∥EF,根据平行线的性质得出即可.
解答 (1)证明:如图①,过点E作EF∥AB,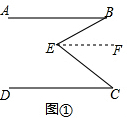
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C=∠CEF.(两直线平行,内错角相等),
∵EF∥AB,
∴∠B=∠BEF(同理),
∴∠B+∠C=∠BEF+∠CEF(等量代换)
即∠B+∠C=∠BEC,
故答案为:平行于同一直线的两直线平行,两直线平行,内错角相等,∠BEF+∠CEF;
(2)证明:如图②,过点E作EF∥AB,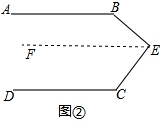
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C+∠CEF=180°,∠B+∠BEF=180°,
∴∠B+∠C+∠AEC=360°,
∴∠B+∠C=360°-∠BEC;
(3)解:如图③,过点E作EF∥AB,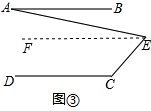
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C+∠CEF=180°,∠A=∠BEF,
∵∠C=120°,∠AEC=80°,
∴∠CEF=180°-120°=60°,
∴∠BEF=80°-60°=20°,
∴∠A=∠BEF=20°.
故答案为:20°.
点评 本题考查了平行线的性质和判定的应用,能正确作出辅助线是解此题的关键,注意:①两直线平行,内错角相等,②两直线平行,同位角相等,③两直线平行,同旁内角互补.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
7.如果a,b表示两个实数,那么下列命题正确的是( )
| A. | 若a2=b2,则a=b | B. | 若a<b,则$\sqrt{{a}^{2}}<\sqrt{{b}^{2}}$ | C. | 若$\root{3}{a}$=$\root{3}{b}$,则$\sqrt{a}=\sqrt{b}$ | D. | 若a>b,则$\root{3}{a}$$>\root{3}{b}$ |
4.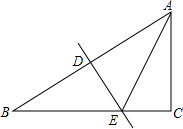 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )
 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )| A. | 16 | B. | 14 | C. | 12 | D. | 10 |
11.若a2+2ka+9是一个完全平方公式的展开式,则k等于( )
| A. | 3 | B. | ±6 | C. | -6 | D. | ±3 |
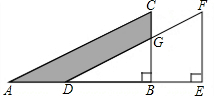 如图,将直角三角形ABC沿AB方向平移AD的长度得到三角形DEF,已知BE=5,EF=8,CG=4,则图中阴影部分的面积为30.
如图,将直角三角形ABC沿AB方向平移AD的长度得到三角形DEF,已知BE=5,EF=8,CG=4,则图中阴影部分的面积为30.