题目内容
16.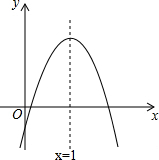 二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b<0;②c<0;③4a+2b+c>0;④(a+c)2<b2;⑤b+2a=0;其中正确的是①②④⑤(填序号)
二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b<0;②c<0;③4a+2b+c>0;④(a+c)2<b2;⑤b+2a=0;其中正确的是①②④⑤(填序号)
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①如图所示,抛物线开口方向向上,则a>0;
对称轴x=-$\frac{b}{2a}$=1,则b=-2a<0,即b<0.故①正确;
②由图象交y轴于负半轴可知,c<0.故②正确;
③根据图示知,当x=0时,y<0.根据抛物线的对称性得到当x=2与当x=0时所对应的y值相等,即当x=2时,y<0.所以,4a+2b+c<0.故③错误;
④由图示知,当x=1时,y>0.即a+b+c>0.当x=-1时,y<0.即a-b+c<0.
所以(a-b+c)(a+b+c)<0,
所以(a+c)2-b2<0,即(a+c)2<b2.故④正确.
⑤对称轴x=-$\frac{b}{2a}$=1,则b=-2a,即b+2a=0.故⑤正确.
故答案是:①②④⑤.
点评 本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
6.在直角坐标系中,一条直线平行y轴,且到y轴的距离为2,点P(x,y)在该直线上,那么下列说法正确的是( )
| A. | x=2 | B. | y=2 | C. | x=±2 | D. | y=±2 |
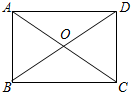 如图,在矩形ABCD中,对角线AC与BD相交于点O,且AB=OA=2cm,则AD的长为2$\sqrt{3}$cm.
如图,在矩形ABCD中,对角线AC与BD相交于点O,且AB=OA=2cm,则AD的长为2$\sqrt{3}$cm.
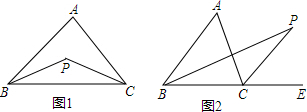
 如图所示,在△ABC中,AB=AC,在AB上取一点E,在AC延长线上取一点F,使BE=CF,EF交BC于G.求证:EG=FG.
如图所示,在△ABC中,AB=AC,在AB上取一点E,在AC延长线上取一点F,使BE=CF,EF交BC于G.求证:EG=FG.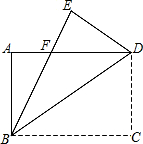 如图,有一个直角三角形纸片,两直角边AB=6cm,BC=8cm,现将直角边BC沿直线BD折叠,使点C落在点E处,求三角形BDF的面积是多少?
如图,有一个直角三角形纸片,两直角边AB=6cm,BC=8cm,现将直角边BC沿直线BD折叠,使点C落在点E处,求三角形BDF的面积是多少?