题目内容
3．
将如图所示的图形面积分成相等的两部分．
分析 根据平行四边形和圆的对称性可知当直线过平行四边形对角线的交点和圆的圆心就可把图形面积分成相等的两部分的．
解答 
解：
由平行四边形的对称性可知当直线过对角线的交点时，可把平行四边形分成面积相等的两部分，
当直线过圆心时，把圆的面积分成相等的两部分，
∴当直线过平行四边形的对角线的交点和圆的圆心时即可把图形分成面积相等的两部分，
如图所示．
点评 本题主要考查图形的对称性，掌握平行四边形和圆的对称性是解题的关键．
练习册系列答案
相关题目
11．
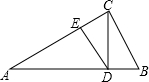如图，在Rt△ABC中，BC=a，AB=c，CD为斜边上的高，DE⊥AC．设△AED、△CDB、△ABC的周长分别为p1，p2，p，则当$\frac{{p}_{1}+{p}_{2}}{p}$取最大值时，sinA=（ ）
如图，在Rt△ABC中，BC=a，AB=c，CD为斜边上的高，DE⊥AC．设△AED、△CDB、△ABC的周长分别为p1，p2，p，则当$\frac{{p}_{1}+{p}_{2}}{p}$取最大值时，sinA=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{3}{4}$ |
如图，在平面直角坐标系中，⊙P的半径为4，圆心P坐标是（4，a）（a＞4），函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{3}$，则a的值是4+2$\sqrt{2}$．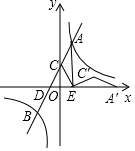
已知一次函数y1=k1x+b与反比例函数y2=$\frac{{k}_{2}}{x}$相交于点A、B，与y轴交于点C，与x轴交于点D，过点A作AE⊥x轴于点E，点O为DE中点，连接CE，已知S△ADE=4，tan∠DCO=$\frac{1}{2}$．