题目内容
6.已知y是x的反比例函数,且在每个象限内,y随x的增大而减小.请写出一个满足以上条件的函数表达式y=$\frac{2}{x}$(k>0即可).分析 首先根据反比例函数的性质可得k>0,再写一个符合条件的数即可.
解答 解:∵反比例函数$y=\frac{k}{x}$(k是常数,k≠0),在其图象所在的每一个象限内,y的值随着x的值的增大而减小,
∴k>0,
∴y=$\frac{2}{x}$,
故答案为:y=$\frac{2}{x}$.
点评 此题主要考查了反比例函数的性质,关键是掌握对于反比例函数$y=\frac{k}{x}$.当k>0时,在每一个象限内,函数值y随自变量x的增大而减小;当k<0时,在每一个象限内,函数值y随自变量x增大而增大.

练习册系列答案
相关题目
14. 如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BAD的度数是( )
如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BAD的度数是( )
 如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BAD的度数是( )
如图,四边形ABCD内接于⊙O,∠BCD=120°,则∠BAD的度数是( )| A. | 30° | B. | 60° | C. | 80° | D. | 120° |
1.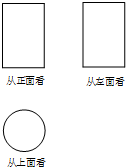 如图分别是从正面、左面、上面看某几何体所得的平面图形,则该几何体是( )
如图分别是从正面、左面、上面看某几何体所得的平面图形,则该几何体是( )
 如图分别是从正面、左面、上面看某几何体所得的平面图形,则该几何体是( )
如图分别是从正面、左面、上面看某几何体所得的平面图形,则该几何体是( )| A. | 长方体 | B. | 四棱锥 | C. | 圆锥 | D. | 圆柱 |
18.点A为直线l外一点,点B在直线l上,若AB=3厘米,则点A到直线l的距离( )
| A. | 大于3厘米 | B. | 等于3厘米 | C. | 小于3厘米 | D. | 小于或等于3厘米 |
15.若|a|=3,|b|=1,则代数式a+b的值是( )
| A. | 4 | B. | -4 | C. | 2或-2 | D. | ±2或±4 |
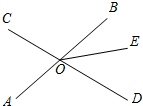 如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.
如图,直线AB、CD相交于点O,∠AOC=72°,射线OE在∠BOD的内部,∠DOE=2∠BOE.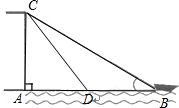 已知:如图,有人在岸上点C的地方,用绳子拉船靠岸,开始时,绳长CB=10米,CA⊥AB,且CA=6米,拉动绳子将船从点B沿BA方向行驶到点D后,绳长CD=6$\sqrt{2}$米.
已知:如图,有人在岸上点C的地方,用绳子拉船靠岸,开始时,绳长CB=10米,CA⊥AB,且CA=6米,拉动绳子将船从点B沿BA方向行驶到点D后,绳长CD=6$\sqrt{2}$米.