题目内容
19.某函数具有下列两条性质:(1)它的图象是经过原点(0,0)的一条直线;(2)y的值随x值的增大而增大.请你举出一个满足上述条件的函数y=2x(答案不唯一).(用关系式表示)分析 直接根据正比例函数的性质即可得出结论.
解答 解:设正比例函数的解析式为y=kx(k≠0),
∵y的值随x值的增大而增大,
∴k>0,
∴此函数的解析式可以为y=2x(答案不唯一).
故答案为:y=2x(答案不唯一).
点评 本题考查的是正比例函数的性质,熟知正比例函数的解析式为y=kx(k≠0)中,当k>0时,y的值随x值的增大而增大是解答此题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
7.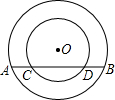 如图,以点O为圆心的两个圆中,大圆的弦AB交小圆于点C,D,已知AB=4,CD=2,点O到弦AB的距离等于1,那么这两个圆的半径之比为( )
如图,以点O为圆心的两个圆中,大圆的弦AB交小圆于点C,D,已知AB=4,CD=2,点O到弦AB的距离等于1,那么这两个圆的半径之比为( )
 如图,以点O为圆心的两个圆中,大圆的弦AB交小圆于点C,D,已知AB=4,CD=2,点O到弦AB的距离等于1,那么这两个圆的半径之比为( )
如图,以点O为圆心的两个圆中,大圆的弦AB交小圆于点C,D,已知AB=4,CD=2,点O到弦AB的距离等于1,那么这两个圆的半径之比为( )| A. | 3:2 | B. | $\sqrt{5}$:2 | C. | $\sqrt{5}$:$\sqrt{2}$ | D. | 5:4 |
14.有六张卡片,正面分别画有下列图形:①角;②正三角形;③平行四边形;④等腰梯形;⑤圆;⑥菱形.将卡片背面向上洗匀,从中随机抽取一张,正面图形一定满足既是轴对称图形,又是中心对称图形的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
9.已知代数式2x2-x+6的值是8,那么代数式6x2-3x-2的值为( )
| A. | -$\frac{4}{3}$ | B. | -$\frac{8}{3}$ | C. | 4 | D. | 5 |
 某菜农搭建一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,得抛物线的表达式y=-$\frac{1}{2}{x}^{2}$+2.
某菜农搭建一个横截面为抛物线的大棚,建立如图所示的直角坐标系后,得抛物线的表达式y=-$\frac{1}{2}{x}^{2}$+2.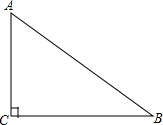 如图,在△ABC中,∠C=90°,用直尺和圆规作BC的垂直平分线l,交斜边AB于点O.
如图,在△ABC中,∠C=90°,用直尺和圆规作BC的垂直平分线l,交斜边AB于点O.