题目内容
10．
某菜农搭建一个横截面为抛物线的大棚，建立如图所示的直角坐标系后，得抛物线的表达式y=-$\frac{1}{2}{x}^{2}$+2．（1）若菜农的身高为1.60米，他在不弯腰的情况下，横向活动的范围是几米？
（2）大棚的高度是多少？
分析 （1）利用函数解析式得出y=1.6m时，x的值得出答案；
（2）求出x=0时y的值即可．
解答 解：（1）当y=1.6m时，1.6=-$\frac{1}{2}$x2+2，
解得：x1=$\frac{2\sqrt{5}}{5}$，x2=-$\frac{2\sqrt{5}}{5}$，
$\frac{2\sqrt{5}}{5}$-（-$\frac{2\sqrt{5}}{5}$）=$\frac{4\sqrt{5}}{5}$（m），
∴菜农的身高为1.60米，他在不弯腰的情况下，横向活动的范围是$\frac{4\sqrt{5}}{5}$米；
（2）当x=0时，y=2，
∴大棚的高度是2m．
点评 此题主要考查了二次函数应用以及一元二次方程的解法，正确理解方程与函数关系是解题关键．
练习册系列答案
相关题目
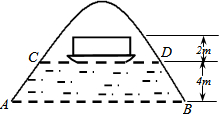去年2月份下旬的某双休日赵化中学组织教职工以及家属游兴文石林时，有几个数学老师发现有一个地下河的进口处是一呈抛物线状的天然拱洞，未涨水时测得水面宽AB是10米，当涨水水面上升4米后，测得水面宽CD为6米．
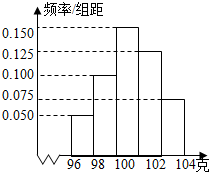如图是抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），[104，106]，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是（ ）