题目内容
7. 在括号内注明依据:
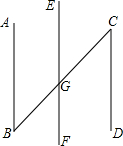
在括号内注明依据:已知,如图,∠B=∠C,AB∥EF,试证明:∠BGF=∠C.
证明:∵∠B=∠C(已知)
∴AB∥CD(内错角相等,两直线平行)
又∵AB∥EF(已知)
∴EF∥CD(平行于同一直线的两直线平行)
∴∠BGF=∠C(两直线平行,同位角相等).
分析 根据平行线的判定推出AB∥CD,求出EF∥CD,根据平行线的性质推出即可.
解答 证明:∵∠B=∠C(已知),
∴AB∥CD(内错角相等,两直线平行),
∵AB∥EF(已知),
∴EF∥CD(平行于同一直线的两直线平行),
∴∠BGF=∠C(两直线平行,同位角相等),
故答案为:(已知),(内错角相等,两直线平行),(已知),(平行于同一直线的两直线平行),(两直线平行,同位角相等).
点评 本题考查了对平行线的性质和判定的应用,能正确运用定理进行推理是解此题的关键,注意:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行,反之亦然.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
12.某校举办了以“爱国、敬业、诚实、友善”为主题的演讲比赛,徐老师为鼓励同学们,带了70元钱去购买甲、乙两种笔记本作为奖品.已知甲种笔记本每车5元,乙种笔记本每本4元,每种笔记本至少买2本,且恰好用完70元钱,则张老师购买笔记本的方案共有( )
| A. | 2种 | B. | 3种 | C. | 4种 | D. | 5种 |
19.计算$\sqrt{2}$($\sqrt{6}$÷$\sqrt{3}$)的结果是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
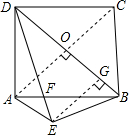 正方形ABCD中,AE∥BD,DE=DB,求证:BF=BE.
正方形ABCD中,AE∥BD,DE=DB,求证:BF=BE. 如图,AE=CF,AD∥BC,AD=CB.求证:△ADF≌△CBE.
如图,AE=CF,AD∥BC,AD=CB.求证:△ADF≌△CBE.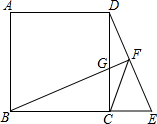 如图,点E为正方形ABCD的边BC延长线上一点,BF⊥DE于点F,交CD边于点G.
如图,点E为正方形ABCD的边BC延长线上一点,BF⊥DE于点F,交CD边于点G.