题目内容
 如图,四边形ABCD是周长为40的菱形,点A的坐标是(0,8),则点B的坐标为
如图,四边形ABCD是周长为40的菱形,点A的坐标是(0,8),则点B的坐标为考点:菱形的性质,坐标与图形性质
专题:
分析:本题可根据菱形的四边相等的性质以及菱形的周长可求出边长的值,再根据勾股定理即可求出OB的长,进而可求出点B的坐标.
解答::解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵菱形ABCD是周长为40,
∴AB=
×40=10,
∵点A的坐标是(0,8),
∴AO=8,
∴BO=
=6,
∴点B的坐标为(-6,0),
故答案为:(-6,0).
∴AB=BC=CD=AD,
∵菱形ABCD是周长为40,
∴AB=
| 1 |
| 4 |
∵点A的坐标是(0,8),
∴AO=8,
∴BO=
| 102-82 |
∴点B的坐标为(-6,0),
故答案为:(-6,0).
点评:本题考查了菱形的性质、坐标与图形的性质以及勾股定理.在直角坐标系中,运用菱形的性质,四边相等,对角线互相垂直平分,根据点的坐标确定相关线段的长度,运用勾股定理求解.

练习册系列答案
相关题目
 实数a,b在数轴上的位置如图所示,则化简|b-a|+|a|+|b|的结果为( )
实数a,b在数轴上的位置如图所示,则化简|b-a|+|a|+|b|的结果为( )| A、2a | B、2b |
| C、2b-2a | D、0 |
下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④三边的高又是它的中线的三角形,其中是等边三角形的个数为( )
| A、1 | B、2 | C、3 | D、4 |
 如图,直线AB与直线CD交于点O,OE⊥AB,OF平分∠AOC,若∠BOD=70°.则∠EOF的度数为( )
如图,直线AB与直线CD交于点O,OE⊥AB,OF平分∠AOC,若∠BOD=70°.则∠EOF的度数为( )| A、115° | B、125° |
| C、135° | D、145° |
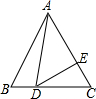 如图,D为等边△ABC边BC上一点,∠ADE=60°,交AC于E,若BD=2,CD=3,则CE=
如图,D为等边△ABC边BC上一点,∠ADE=60°,交AC于E,若BD=2,CD=3,则CE=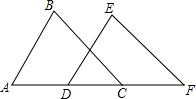 如图,已知AB∥DE,BC∥EF,C在AF上,且AD=CF,△ABC与△DEF全等吗?请说明理由.
如图,已知AB∥DE,BC∥EF,C在AF上,且AD=CF,△ABC与△DEF全等吗?请说明理由.