题目内容
等腰三角形底边长为10cm，周长为36cm，则底角的正弦值为 ．
考点：解直角三角形
专题：
分析：根据等腰三角形的周长，底边长，可得腰长，根据勾股定理，可得底边上的高，根据正弦函数的定义，可得答案．
解答：解：如图：
，
由等腰三角形的性质相等，得
AB=（36-10）÷2=13（cm），BD=5（cm）．
在Rt△ABD中由勾股定理，得
AD=
=
=
=12（cm）
由正弦函数定义，得sin∠B=
=
，
故答案为：
．
，由等腰三角形的性质相等，得
AB=（36-10）÷2=13（cm），BD=5（cm）．
在Rt△ABD中由勾股定理，得
AD=
| AB2-BD2 |
| 132-52 |
| 144 |
由正弦函数定义，得sin∠B=
| AD |
| AB |
| 12 |
| 13 |
故答案为：
| 12 |
| 13 |
点评：本题考查了解直角三角形，利用了等腰三角形的性质，正弦函数的定义．
练习册系列答案
阅读快车系列答案
相关题目
在△ABC中，AB=AC，若AC的垂直平分线DE交AC于点D，交BC于点E，且∠BAE=90°，则∠B为（ ）
| A、60° | B、30° |
| C、45° | D、无法确定 |
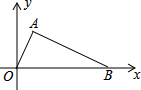如图，已知A（1，2），B（5，0），O（0，0），试判断△ABO的形状，并说明理由．
如图，直线L：与x轴、y轴分别交于A（4，0）、B（0，2）两点，在y轴上有一点C（0，4），动点M从A点以每秒1个单位的速度沿x轴向左移动．