题目内容
14.我们把a、b两个数的较大数记作Z{a,b},一次函数y=-x+m与函数y=Z{x+2,x2}的图象有且只有2个交点,则m的取值或范围为m≥0或-$\frac{1}{4}$.分析 结合x的范围画出函数y=Z{x+2,x2}的图象,由直线y=-x+m与该函数图象只有两个交点且,判断直线的位置得①直线y=y=-x+m经过点(-1,1)时可以求出m;②直线y=y=-x+m与函数y=x2相切时,可以求出m.
解答 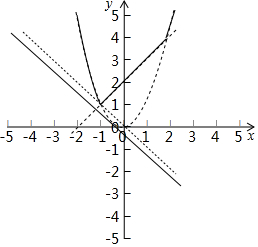 解:根据题意,x2<x+2,即x2-x-2<0,
解:根据题意,x2<x+2,即x2-x-2<0,
解得:-1<x<2,
故当-1<x<2时,y=x+2;
当x≤-1或x≥2时,y=x2;
函数图象如下:
由图象可知,∵直线y=-x+m与函数y=Z{x+2,x2}的图象有且只有2个交点,且k<0,
①直线y=-x+m经过点(-1,1)时,1=1+m,m=0,此时直线y=-x与函数y=Z{x+2,x2}的图象有且只有2个交点.
②直线y=-x+m与函数y=x2相切时,由$\left\{\begin{array}{l}{y={x}^{2}}\\{y=-x+m}\end{array}\right.$消去y得x2+x-m=0,∵△=0,
∴1+4m=0,
∴m=-$\frac{1}{4}$,此时直线y=-x-$\frac{1}{4}$与函数y=Z{x+2,x2}的图象有且只有2个交点.
③由图象知,当m>0时,直线y=-x-$\frac{1}{4}$与函数y=Z{x+2,x2}的图象有且只有2个交点.
综上,m≥0或-$\frac{1}{4}$时,一次函数y=-x+m与函数y=Z{x+2,x2}的图象有且只有2个交点,
故答案为:m≥0或-$\frac{1}{4}$.
点评 本题主要考查二次函数与一元一次不等式间的关系,根据题意判断直线的位置是关键,学会用转化的思想解决问题,属于中考填空题中的压轴题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
3.计算2x3÷$\frac{1}{x}$的结果是( )
| A. | 2x2 | B. | 2x4 | C. | 2x | D. | 4 |
4.下列每组数分别表示三根木棒的长度,首尾顺次相接可以构成直角三角形的一组是( )
| A. | 4,5,6 | B. | 1.5,2,2.5 | C. | 2,3,4 | D. | 1,$\sqrt{2}$,3 |
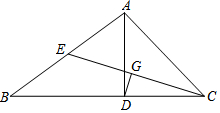 已知:如图,在△ABC中,AD是BC边上的高,∠B=30°,∠ACB=45°,CE是AB边上的中线.
已知:如图,在△ABC中,AD是BC边上的高,∠B=30°,∠ACB=45°,CE是AB边上的中线.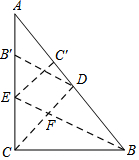 如图,在 Rt△ABC中,∠ACB=90°,BC=3,AC=4,沿CD折叠,使点B落在CA边上的B'处,展开后,再沿BE折叠,使点C落在BA边上的C'处,CD与BE交于点F.
如图,在 Rt△ABC中,∠ACB=90°,BC=3,AC=4,沿CD折叠,使点B落在CA边上的B'处,展开后,再沿BE折叠,使点C落在BA边上的C'处,CD与BE交于点F.