题目内容
9.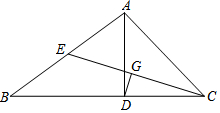 已知:如图,在△ABC中,AD是BC边上的高,∠B=30°,∠ACB=45°,CE是AB边上的中线.
已知:如图,在△ABC中,AD是BC边上的高,∠B=30°,∠ACB=45°,CE是AB边上的中线.(1)CD=$\frac{1}{2}$AB;
(2)若CG=EG,求证:DG⊥CE.
分析 (1)含30°角的直角三角形的性质得出AD=$\frac{1}{2}$AB,证得△ACD是等腰直角三角形,得出CD=AD,即可得出结论;
(2)连接DE,证得DE是Rt△ABD斜边AB上的中线,得出DE=$\frac{1}{2}$AB,证得DE=CD,即可得出结论.
解答 证明:(1)∵AD是BC边上的高,
∴AD⊥BC,
∵∠B=30°,
∴AD=$\frac{1}{2}$AB,
∵∠ACB=45°,
∴△ACD是等腰直角三角形,
∴CD=AD,
∴CD=$\frac{1}{2}$AB;
(2)连接DE,如图所示: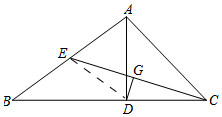
∵CE是AB边上的中线,AD⊥BC,
∴DE是Rt△ABD斜边AB上的中线,
∴DE=$\frac{1}{2}$AB,
∵CD=$\frac{1}{2}$AB,
∴DE=CD,
∵CG=EG,
∴DG⊥CE.
点评 本题主要考查了含30度角的直角三角形的性质、等腰三角形的判定与性质、直角三角形斜边上的中线定理等知识;熟练掌握直角三角形中,斜边上的中线等于斜边的一半、等腰三角形的三线合一是解决问题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
19.若∠α的补角是∠α的2倍,则∠α的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
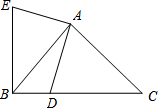 在等腰 Rt△ABC中,∠A=90°,AC=AB=2,D是BC边上的点且BD=$\frac{1}{3}$CD,连接AD.AD⊥AE,AE=AD,连接BE.下列结论:
在等腰 Rt△ABC中,∠A=90°,AC=AB=2,D是BC边上的点且BD=$\frac{1}{3}$CD,连接AD.AD⊥AE,AE=AD,连接BE.下列结论:
 如图,已知直线m的解析式为y=-$\frac{1}{2}$x+1,与x轴、y轴分别交于A,B两点,以线段AB为直角边在第一象限内作等腰Rt△ABC,且∠BAC=90°,点P为直线x=1上的动点,且△ABP的面积与△ABC的面积相等.
如图,已知直线m的解析式为y=-$\frac{1}{2}$x+1,与x轴、y轴分别交于A,B两点,以线段AB为直角边在第一象限内作等腰Rt△ABC,且∠BAC=90°,点P为直线x=1上的动点,且△ABP的面积与△ABC的面积相等.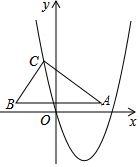 如图,在平面直角坐标系xOy中,Rt△ABC的直角顶点C在抛物线y=ax2+bx上运动,斜边AB垂直于y轴,且AB=8,∠ABC=60°,当Rt△ABC的斜边AB落在x轴上时,B点坐标是(-3,0),A点恰在抛物线y=ax2+bx上
如图,在平面直角坐标系xOy中,Rt△ABC的直角顶点C在抛物线y=ax2+bx上运动,斜边AB垂直于y轴,且AB=8,∠ABC=60°,当Rt△ABC的斜边AB落在x轴上时,B点坐标是(-3,0),A点恰在抛物线y=ax2+bx上