题目内容
5.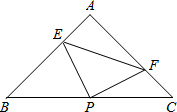 如图,在等腰直角三角形ABC中,P为斜边BC的中点,以P为顶点的直角的两边分别与边AB,AC交于点E,F,连接EF,当∠EPF旋转时(点E不与A,B重合),试探究PE,PF,EF之间的数量关系.
如图,在等腰直角三角形ABC中,P为斜边BC的中点,以P为顶点的直角的两边分别与边AB,AC交于点E,F,连接EF,当∠EPF旋转时(点E不与A,B重合),试探究PE,PF,EF之间的数量关系.
分析 PE=PF=$\frac{\sqrt{2}}{2}$EF;只要证明△PEF是等腰直角三角形即可,即证明∠EPF=90°,PE=PF.连接AP,证线△BPE≌△APF即可.段相等通常是证明线段所在的三角形全等.而等腰三角形最常用的辅助线是用“三线合一”作辅助线,构造三角形全等.
解答 解:PE=PF=$\frac{\sqrt{2}}{2}$EF;
理由如下:
连接AP,
∵PA是等腰直角△ABC底边上的中线,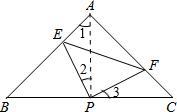
∴PA⊥PC(等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(三线合一)).
又∵AB⊥AC,
∴∠1=90°-∠PAC,∠C=90°-∠PAC,
∴∠1=∠C(等量代换).
同理可得PA⊥PC,PE⊥PF,
∴∠2=90°-∠APF,∠3=90°-∠APF,
∴∠2=∠3.
由PA是Rt△ABC斜边上的中线,得:
PA=$\frac{1}{2}$BC=PC(直角三角形斜边上的中线等于斜边的一半).
在△PAE和△PCF中,
$\left\{\begin{array}{l}{∠1=∠C}\\{PA=PC}\\{∠2=∠3}\end{array}\right.$,
∴△PAE≌△PCF(ASA).
∴PE=PF(全等三角形对应边相等),
∴△PEF是等腰直角三角形,
∴PE=PF=$\frac{\sqrt{2}}{2}$EF.
点评 本题主要考查了全等三角形的判定与性质以及等腰直角三角形的性质,证明线段相等通常是证明线段所在的三角形全等.而等腰三角形最常用的辅助线是用“三线合一”作辅助线,构造三角形全等.

练习册系列答案
相关题目
16.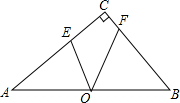 如图,Rt△ACB中,∠ACB=90°,O为AB的中点,AE=AO,BF=BO,OE=2$\sqrt{2}$,OF=3,则AB的长为( )
如图,Rt△ACB中,∠ACB=90°,O为AB的中点,AE=AO,BF=BO,OE=2$\sqrt{2}$,OF=3,则AB的长为( )
 如图,Rt△ACB中,∠ACB=90°,O为AB的中点,AE=AO,BF=BO,OE=2$\sqrt{2}$,OF=3,则AB的长为( )
如图,Rt△ACB中,∠ACB=90°,O为AB的中点,AE=AO,BF=BO,OE=2$\sqrt{2}$,OF=3,则AB的长为( )| A. | $\sqrt{58}$ | B. | 5 | C. | 8 | D. | $\sqrt{29}$ |
13.设a,b是方程x2+x-2015=0的两个不相等的实数根,a2+6a+5b-2000的值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 10或11 |
17.将二次函数y=2x2-4x+1化成顶点式是( )
| A. | y=2(x+1)2-1 | B. | y=2(x-1)2-1 | C. | y=2(x+1)2+1 | D. | y=2(x-1)2+1 |
 如图所示,在Rt△ABC中,∠C=90°,D为BC边上一点且BD=2CD,连接AD并延长至E,使得AD=DE,求证:BE=$\frac{1}{2}$AE.
如图所示,在Rt△ABC中,∠C=90°,D为BC边上一点且BD=2CD,连接AD并延长至E,使得AD=DE,求证:BE=$\frac{1}{2}$AE.