题目内容
16．一种商品进价为每件8元，如果售价为每件10元，一周可卖出55件．市场调查表明：这种商品如果每件涨价1元，每周要少卖5件；每件降价1元，每周要多卖5件．（1）求销售该商品所获利润y（元）与上涨价格x（元）之间的函数关系式；
（2）求涨价多少元时，所获利润最大？最大利润是多少？
分析 （1）依题意利润=单件利润×销售件数，可得y与x的函数关系式；
（2）把函数关系式用配方法化为顶点式，根据二次函数的性质分析即可．
解答 解：（1）设涨价x元，利润为y元，则
y=（10-8+x）（55-5x）=-5x2+45x+110；
（2）y=-5x2+45x+110=-5${（x-\frac{9}{2}）^2}+\frac{845}{4}$，
因为x取整数，-5＜0，所以当x=4或5时，y最大，即涨价4元或5元时，最大利润是210元．
点评 此题主要考查了二次函数的应用以及二次函数最值求法等知识，得出y与x的函数关系式是解题关键．
练习册系列答案
相关题目
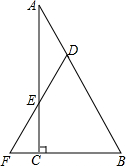如图，在Rt△ABC中，在斜边AB和直角边AC上分别取一点D，E，使DE=DA，延长DE交BC的延长线于点F．△DFB是等腰三角形吗？请说明你的理由．
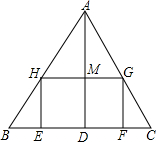如图，△ABC，是一张锐角三角形的硬纸片，AD是边BC上的高，BC=40cm，AD=30cm，从这张硬纸片上剪下一个矩形EFGH，使它的一边EF在BC上，顶点G、H分别在AC，AB上，AD与HG的交点为M．
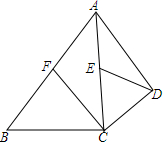如图，在四边形ABCD中，$\frac{BC}{CD}$=$\frac{3}{2}$，AC平分∠BAD，∠ACB=∠ADC=90°，CF和DE是△ABC、△ACD的中线，求$\frac{CE}{DE}$的值．
如图，在Rt△ABC中，∠C=90°，正方形DEFG的顶点D，E在AB边上，F，G分别在BC和AC上，若AD=4，BE=1，求：
如图，已知$\frac{AD}{AB}$=$\frac{DE}{BC}$=$\frac{AE}{AC}$，求证：∠ABD=∠ACE．