题目内容
1.已知$\frac{a+b-c}{c}$=$\frac{a-b+c}{b}$=$\frac{-a+b+c}{a}$,且abc≠0,求$\frac{(a+b)(b+c)(a+c)}{abc}$的值.分析 设$\frac{a+b-c}{c}$=$\frac{a-b+c}{b}$=$\frac{-a+b+c}{a}$=k,得出a+b-c=ck①,a-b+c=bk②,-a+b+c=ak③,①+②+③得a+b+c=(a+b+c)k,求得k=1,由①得a+b=(k+1)c,由②得a+c=(k+1)b,由③得b+c=(k+1)a,代入所求分式即可得出答案.
解答 解:设$\frac{a+b-c}{c}$=$\frac{a-b+c}{b}$=$\frac{-a+b+c}{a}$=k,
则a+b-c=ck①,a-b+c=bk②,-a+b+c=ak③,
由①得a+b=(k+1)c,由②得a+c=(k+1)b,由③得b+c=(k+1)a,
①+②+③得a+b+c=(a+b+c)k,
所以k=1,
把a+b=(k+1)c,a+c=(k+1)b,b+c=(k+1)a代入,
原式=$\frac{(k+1)^{3}abc}{abc}$=(k+1)3=23=8.
点评 本题考查了分式的混合运算,属于基础题,主要是由已知条件先变形后再代入化简.

练习册系列答案
相关题目
13. 如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
 如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )
如图,直角△ABC沿直角边BC所在的直线向右平移得到△DEF,则下列结论中错误的是( )| A. | ∠ACB=∠DFE | B. | BE=CF | C. | AB∥DE | D. | AG=CG |
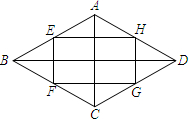 如图,顺次连接菱形ABCD的各边中点E,F,G,H,若AC=6,BD=12,则四边形EFGH的面积为18.
如图,顺次连接菱形ABCD的各边中点E,F,G,H,若AC=6,BD=12,则四边形EFGH的面积为18. 如图,在Rt△ACB内作边长依次为m、n、p(m>n>p)的三个正方形,设BC=a,AC=b.
如图,在Rt△ACB内作边长依次为m、n、p(m>n>p)的三个正方形,设BC=a,AC=b.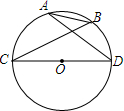 如图,在⊙O中,CD为直径,CD=3,AB=1.求cosα的值.
如图,在⊙O中,CD为直径,CD=3,AB=1.求cosα的值.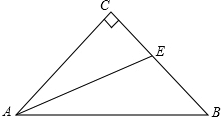 如图,等腰△ABC中,∠ACB=90°,I为△ABC的内心,AI的延长线交BC于E.若IE=1,则AI=1+$\sqrt{2}$.
如图,等腰△ABC中,∠ACB=90°,I为△ABC的内心,AI的延长线交BC于E.若IE=1,则AI=1+$\sqrt{2}$. 如图,在菱形ABCD中,AB=2,∠C=60°,E是边AD中点,F是边AB上一点(不与点A重合)延长FE交CD的延长线于点G,连接FD,AG.
如图,在菱形ABCD中,AB=2,∠C=60°,E是边AD中点,F是边AB上一点(不与点A重合)延长FE交CD的延长线于点G,连接FD,AG. 如图,点E、F位于正方形ABCD边BC、CD上,且BE:EC=2:1,∠EAF=30°,则CF:FD=$\frac{1+13\sqrt{3}}{23}$.
如图,点E、F位于正方形ABCD边BC、CD上,且BE:EC=2:1,∠EAF=30°,则CF:FD=$\frac{1+13\sqrt{3}}{23}$.