题目内容
2. 已知a,b,c在数轴上对应点的位置如图所示,化简:|a|-|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|.
已知a,b,c在数轴上对应点的位置如图所示,化简:|a|-|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|.
分析 根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义与二次根式的性质化简,去括号合并即可得到结果.
解答 解:根据数轴上点的位置得:b<a<0<c,
∴a+b<0,c-a>0,b-c<0,
∴|a|-|a+b|-$\sqrt{(c-a)^{2}}$+|b-c|
=-a+a+b-c+a-b+c
=a.
点评 此题考查了整式的加减,实数与数轴,二次根式的性质与化简,以及绝对值,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握运算法则是解本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
7.下列是关于变量x和y的四个关系式:①y=x,②y2=x,③2x2=y,④|y|=2x,其中y是x的函数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
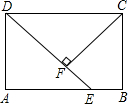 如图,四边形ABCD是矩形,E是AB上一点,且DE=AB,过点C作CF⊥DE,垂足为E.
如图,四边形ABCD是矩形,E是AB上一点,且DE=AB,过点C作CF⊥DE,垂足为E. 如图,AB、CD交于点O,OE⊥AB,OF平分∠BOC,∠AOC:∠BOF=1:1,求∠DOE的度数.
如图,AB、CD交于点O,OE⊥AB,OF平分∠BOC,∠AOC:∠BOF=1:1,求∠DOE的度数.