题目内容
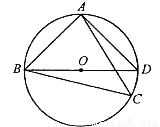
如图,
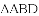
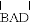 上,且不与点
上,且不与点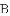
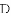
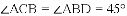
(1)求证: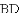
(2)连接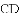
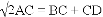 ;
;
(3)若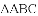
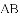
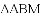
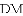
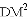 、
、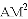 、
、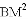 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
如图,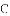
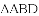
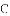
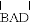 上,且不与点
上,且不与点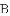
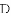
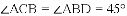
(1)求证: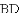
(2)连接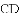
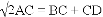 ;
;
(3)若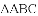
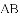
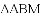
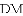
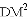 、
、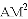 、
、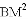 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案