题目内容
7.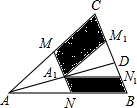 如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为( )
如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为( )| A. | 14 | B. | 21 | C. | 28 | D. | 7 |
分析 根据三角形中位线定理得到MN∥BC,MN=$\frac{1}{2}$BC,得到△AMN∽△ACB,根据相似三角形的性质和平移的性质计算即可.
解答 解:∵M、N分别是△ABC的边AC和AB的中点,
∴MN∥BC,MN=$\frac{1}{2}$BC,
∴△AMN∽△ACB,相似比为1:4,
∵△AMN的面积为7,
∴△ABC的面积为28,
由平移的性质可知,△AMN的面积=△A1M1N1的面积=7,
∴图中阴影部分的面积为28-7-7=14,
故选:A.
点评 本题考查的是三角形中位线定理和相似三角形的性质以及平移的性质,三角形的中位线平行于第三边,并且等于第三边的一半、把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.

练习册系列答案
相关题目
15.在-1,0,-2,1这四个数中,最大的数是( )
| A. | -4 | B. | -2 | C. | 0 | D. | 1 |
12. 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )
 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )
如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )| A. | 20° | B. | 30° | C. | 35° | D. | 40° |
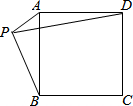 如图,P是正方形ABCD外一点,PA=$\sqrt{2}$,PB=4,则PD长度的最大值为6.
如图,P是正方形ABCD外一点,PA=$\sqrt{2}$,PB=4,则PD长度的最大值为6.
 直线AB、CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,求∠EOB的度数.
直线AB、CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,求∠EOB的度数.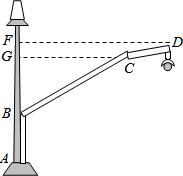 如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,AB=25cm,CG⊥AF,FD⊥AF,点G、点F分别是垂足,BG=40cm,GF=7cm,∠ABC=120°,∠BCD=160°,请计算钢管ABCD的长度.(钢管的直径忽略不计,结果精确到1cm.参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
如图,马路边安装的路灯由支柱上端的钢管ABCD支撑,AB=25cm,CG⊥AF,FD⊥AF,点G、点F分别是垂足,BG=40cm,GF=7cm,∠ABC=120°,∠BCD=160°,请计算钢管ABCD的长度.(钢管的直径忽略不计,结果精确到1cm.参考数据:sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)