题目内容
1.观察下列算式,你发现了什么规律?12=$\frac{1×2×3}{6}$;12+22=$\frac{2×3×5}{6}$;12+22+32=$\frac{3×4×7}{6}$;12+22+32+42=$\frac{4×5×9}{6}$;…
(1)根据你发现的规律,计算下面算式的值:12+22+32+…+102=385;
(2)请用一个含n的算式表示这个规律:12+22+32+…+n2=$\frac{n(n+1)(2n+1)}{6}$.
分析 (1)观察不难发现,从1开始的平方数的和,分母都是6,分子为最后一个数与比它大1的数的积再乘以比这个数的2倍大1的数的积;
(2)根据(1)中的规律写出即可.
解答 解:(1)12+22+32+…+102=$\frac{10×11×21}{6}$=385;
(2)12+22+32+…+n2=$\frac{n(n+1)(2n+1)}{6}$.
故答案为:385;$\frac{n(n+1)(2n+1)}{6}$.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
12.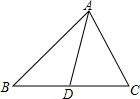 如图,△ACD∽△BCA,则下列各式中一定成立的是( )
如图,△ACD∽△BCA,则下列各式中一定成立的是( )
 如图,△ACD∽△BCA,则下列各式中一定成立的是( )
如图,△ACD∽△BCA,则下列各式中一定成立的是( )| A. | $\frac{AC}{CD}$=$\frac{AB}{BC}$ | B. | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C. | CD2=AD•DB | D. | AC2=CD•BC |
9.下列说法正确的是( )
| A. | -|-2|=-(-2) | B. | (-1)2n=1(n是正整数) | ||
| C. | -(-a-b)=a-b | D. | 2x3y-3x2y-1是三次三项式 |
6.关于x的方程2x+a-10=0与3x-9=0的解相同,则a的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.下列各图中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,已知∠AOB=∠BOC=∠COD,则∠AOB=$\frac{1}{2}$∠AOC,∠BOD=2∠BOC,∠AOC=∠BOD.
如图,已知∠AOB=∠BOC=∠COD,则∠AOB=$\frac{1}{2}$∠AOC,∠BOD=2∠BOC,∠AOC=∠BOD.