题目内容
9.若$\sqrt{x+1}$+(3x+y-1)2=0,求$\sqrt{{y}^{2}-9x}$的平方根.分析 根据非负数的性质列方程求出x、y的值,再求出代数式的值,然后根据平方根的定义解答.
解答 解:由题意得,x+1=0,3x+y-1=0,
解得x=-1,y=4,
所以,$\sqrt{{y}^{2}-9x}$=$\sqrt{{4}^{2}-9×(-1)}$=$\sqrt{25}$=5,
所以,$\sqrt{{y}^{2}-9x}$的平方根是±$\sqrt{5}$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
19.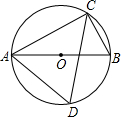 如图,AB是⊙O的直径,∠BAC=25°,则∠ADC=( )
如图,AB是⊙O的直径,∠BAC=25°,则∠ADC=( )
 如图,AB是⊙O的直径,∠BAC=25°,则∠ADC=( )
如图,AB是⊙O的直径,∠BAC=25°,则∠ADC=( )| A. | 25 | B. | 30° | C. | 45° | D. | 65° |
17.如图所示,数轴的单位长度为1,如果点M、N表示的数的绝对值相等,那么点M表示的数是( )


| A. | -4 | B. | -3 | C. | -2 | D. | 3 |
13.在圆心角为120°的扇形AOB中,半径OA=6,则扇形AOB的面积是( )
| A. | 6π | B. | 8π | C. | 12π | D. | 24π |
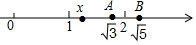
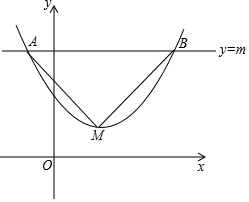 抛物线y=a(x-2)2+3(a>0),直线y=m交抛物线于A、B两点,M为顶点,△ABM为直角三角形,求AB的长.
抛物线y=a(x-2)2+3(a>0),直线y=m交抛物线于A、B两点,M为顶点,△ABM为直角三角形,求AB的长.