题目内容
10.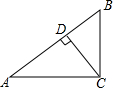 如图,在Rt△ABC中,BC=3,AC=4,CD⊥AB,则CD的长为$\frac{12}{5}$.
如图,在Rt△ABC中,BC=3,AC=4,CD⊥AB,则CD的长为$\frac{12}{5}$.
分析 在直角△ABC中,AB为斜边,已知AC,BC根据勾股定理即可求AB的长度,根据面积法即可求CD的长度.
解答 解:在Rt△ABC中,AB为斜边,AC=3,BC=4,
则AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∵△ABC的面积S=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
解得:CD=$\frac{3×4}{5}$=$\frac{12}{5}$,
故答案为:$\frac{12}{5}$.
点评 本题考查了勾股定理在直角三角形中的运用,考查了直角三角形面积的计算,本题中正确的计算AB的长是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.如果x=-2是关于x的方程3a-2x=7的解,那么a的值是( )
| A. | $a=\frac{11}{3}$ | B. | a=1 | C. | $a=-\frac{1}{2}$ | D. | $a=-\frac{13}{2}$ |
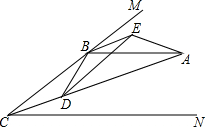 如图,已知CA平分∠MCN,AB∥CN,点D是线段CA上任意点,且BD=BE,∠DBE=∠CBA,连结AE,DE.
如图,已知CA平分∠MCN,AB∥CN,点D是线段CA上任意点,且BD=BE,∠DBE=∠CBA,连结AE,DE. a、b、c三个数在数轴上的位置如图所示,则化简|a-b|-|a-c|的结果是2a-b-c.
a、b、c三个数在数轴上的位置如图所示,则化简|a-b|-|a-c|的结果是2a-b-c.