题目内容
9.计算(1)(7x2y3-8x3y2z)÷8x2y2
(2)3(y-z)2-(2y+z)(-z+2y)
(3)$\frac{{x}^{2}}{x-1}$+$\frac{x}{1-x}$
(2)$\frac{a+1}{{a}^{2}-2a+1}$÷(1+$\frac{2}{a-1}$).
分析 (1)利用同底数幂的除法法则,把括号内的两项分别除以8x2y2即可;
(2)先利用乘法公式展开,然后合并同类项即可;
(3)先化为同分母,再进行同分母的减法运算,然后把分子分解因式后约分即可;
(4)先把括号内通分,再把除法运算化为乘法运算,然后约分即可.
解答 解:(1)原式=$\frac{7}{8}$y-xz;
(2)原式=3(y2-2yz+z2)-(4y2-z2)
=3y2-6yz+3z2-4y2+z2
=-y2-6yz+4z2;
(3)原式=$\frac{{x}^{2}}{x-1}$-$\frac{x}{x-1}$
=$\frac{{x}^{2}-x}{x-1}$
=$\frac{x(x-1)}{x-1}$
=x;
(4)原式=$\frac{a+1}{(a-1)^{2}}$÷$\frac{a-1+2}{a-1}$
=$\frac{a+1}{(a-1)^{2}}$•$\frac{a-1}{a+1}$
=$\frac{1}{a-1}$.
点评 本题考查了整式的混合运算:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.也考查了分式的混合运算.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
19.先化简,再求值
(1)(a2b-2ab2-b3)÷b-(a+b)(a-b),其中a=$\frac{1}{2}$,b=-1.
(2)6x2-(2x-1)(3x-2)+(x+2)(x-2),其中x=3.
(1)(a2b-2ab2-b3)÷b-(a+b)(a-b),其中a=$\frac{1}{2}$,b=-1.
(2)6x2-(2x-1)(3x-2)+(x+2)(x-2),其中x=3.
17.小明到某服装专卖店去做社会调查,了解到该专卖店为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法计算薪资,并获得如下信息:
假设月销售件数为x,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员小张上个月总收入是1700元,则小张上个月卖了多少件服装?
| 营业员 | 小张 | 小王 |
| 月销售件数 | 200 | 150 |
| 月总收入/元 | 1400 | 1250 |
(1)求a、b的值.
(2)若营业员小张上个月总收入是1700元,则小张上个月卖了多少件服装?
19.今年我区吉安镇柑桔喜获丰收,根据柑桔季节性及以往销售经验,销售时间不超过12周,每千克售价y(元)与销售时间x(周)之间的关系如下表:
(1)请你从所学过的一次函数和二次函数中确定哪种函数关系能表达y与x的变化规律(不需说明理由),并写出y关于x的函数关系式.
(2)根据销售经验,第1周每千克售价30元时,当周可以销售1200千克水果;以后售价每降低2元,当周销售量可以增加400千克,通过计算估计最多第几周的销售金额就可以达到60800元.
(3)设第9周的销售量仍满足(2)中的关系,根据销售经验,从第9周后,每周的销售量均比前一周下降900千克,而售价与时间仍满足(1)中的关系,柑桔通过前9周的销售后,只剩5000千克.现准备将这批柑桔全部批发给某水果商,那么每千克的批发价至少为多少元时,才能获得不低于依销售经验按周销售的金额?
(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24,$\sqrt{6}$≈2.45,$\sqrt{7}$≈2.65)
| 销售时间x(周) | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 每千克售价y(元) | 30 | 28 | 26 | 24 | 22 | 20 | … |
(2)根据销售经验,第1周每千克售价30元时,当周可以销售1200千克水果;以后售价每降低2元,当周销售量可以增加400千克,通过计算估计最多第几周的销售金额就可以达到60800元.
(3)设第9周的销售量仍满足(2)中的关系,根据销售经验,从第9周后,每周的销售量均比前一周下降900千克,而售价与时间仍满足(1)中的关系,柑桔通过前9周的销售后,只剩5000千克.现准备将这批柑桔全部批发给某水果商,那么每千克的批发价至少为多少元时,才能获得不低于依销售经验按周销售的金额?
(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24,$\sqrt{6}$≈2.45,$\sqrt{7}$≈2.65)
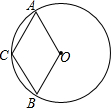 如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号).
如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号).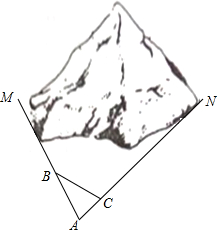 如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离.
如图,M、N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞.工程人员为了计算工程量,必须计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的直线距离. 如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是-5,-π,$\frac{3}{2}$.
如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是-5,-π,$\frac{3}{2}$. 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2. 如图,已知AD是⊙O的直径,AB、BC是⊙O的弦,AD⊥BC,垂足是点E,BC=8,DE=2,求⊙O的半径长和sin∠BAD的值.
如图,已知AD是⊙O的直径,AB、BC是⊙O的弦,AD⊥BC,垂足是点E,BC=8,DE=2,求⊙O的半径长和sin∠BAD的值.