题目内容
20.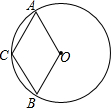 如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号).
如图,四边形ABCO中,点A,B,C在劣弧$\widehat{AB}$上,则下列结论正确的有①②④(在横线上填写所有正确结论的序号).①若四边形ACBO是平行四边形,则四边形ACBO是菱形;
②若四边形ACBO是菱形,则∠AOB=120°;
③若∠AOB=120°,则四边形ACBO是菱形;
④若四边形ACBO是平行四边形,则∠AOB=120°.
分析 根据菱形的判定定理判断即可①;连接AD、BD,根据圆内接四边形的性质和圆周角定理计算出∠AOB的度数,判断②;举出反例判断③;由①②的结论判断④.
解答 解:∵四边形ACBO是平行四边形,又OA=OB,
∴四边形ACBO是菱形,①正确; 如图,连接AD、BD,
如图,连接AD、BD,
由圆周角定理得,∠D=$\frac{1}{2}$∠AOB,
由圆内接四边形的性质得,∠ACB+∠D=180°,
∵四边形ACBO是菱形,
∴∠AOB=∠ACB,
∴∠AOB=120°,②正确;
若∠AOB=120°,则四边形ACBO不一定是菱形,③错误;
四边形ACBO是平行四边形,则四边形ACBO是菱形,则∠AOB=120°,④正确,
故答案为:①②④.
点评 本题考查的是圆周角定理、菱形的判定定理以及平行四边形的性质,灵活运用相关定理、正确作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 如图,过正五边形ABCDE的顶点B作直线l∥AC,则∠1的度数为( )
如图,过正五边形ABCDE的顶点B作直线l∥AC,则∠1的度数为( )
 如图,过正五边形ABCDE的顶点B作直线l∥AC,则∠1的度数为( )
如图,过正五边形ABCDE的顶点B作直线l∥AC,则∠1的度数为( )| A. | 36° | B. | 45° | C. | 55° | D. | 60° |
 如图,有四张背面相同的纸牌.请你用这四张牌计算“24点”,请列出四个符合要求的不同算式.【可运用加、减、乘、除、乘方(例如数2,6,可列62=36或26=64)运算,可用括号;注意:例如4×(1+2+3)=24与(2+1+3)×4=24只是顺序不同,属同一个算式】.
如图,有四张背面相同的纸牌.请你用这四张牌计算“24点”,请列出四个符合要求的不同算式.【可运用加、减、乘、除、乘方(例如数2,6,可列62=36或26=64)运算,可用括号;注意:例如4×(1+2+3)=24与(2+1+3)×4=24只是顺序不同,属同一个算式】.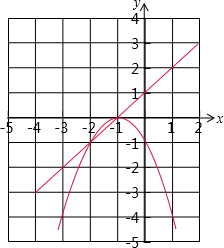 设函数y=(x+1)[(k-2)x+(2k-3)](k是常数).
设函数y=(x+1)[(k-2)x+(2k-3)](k是常数).