Question

4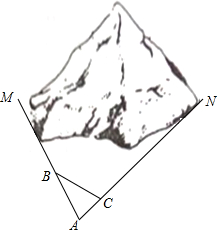．如图，M、N为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线涵洞．工程人员为了计算工程量，必须计算M、N两点之间的直线距离，选择测量点A、B、C，点B、C分别在AM、AN上，现测得AM=1千米、AN=1.8千米，AB=54米、BC=45米、AC=30米，求M、N两点之间的直线距离．

Answer 1

分析 先根据相似三角形的判定得出△ABC∽△ANM，再利用相似三角形的性质解答即可．

解答 解：在△ABC与△AMN中，
$\frac{AC}{AB}=\frac{30}{54}$=$\frac{5}{9}$，$\frac{AM}{AN}=\frac{1000}{1800}$=$\frac{5}{9}$，∴$\frac{AC}{AB}=\frac{AM}{AN}$，又∵∠A=∠A，
∴△ABC∽△ANM，
∴$\frac{BC}{MN}=\frac{AC}{AM}$，即$\frac{45}{MN}=\frac{30}{1000}$，
解得：MN=1500米，
答：M、N两点之间的直线距离是1500米；

点评 此题考查了相似三角形的判定与性质；熟记相似三角形的判定方法是解决问题的关键．