题目内容
4.化简:${(\sqrt{3}+\sqrt{2})}^{2004}$•${(\sqrt{3}-\sqrt{2})}^{2005}$.分析 首先把原式化成=[${(\sqrt{3}+\sqrt{2})}^{2004}$•($\sqrt{3}$-$\sqrt{2}$)2004]•($\sqrt{3}$-$\sqrt{2}$),再根据平方差公式进行计算,即可得出答案.
解答 解:${(\sqrt{3}+\sqrt{2})}^{2004}$•${(\sqrt{3}-\sqrt{2})}^{2005}$.
=[${(\sqrt{3}+\sqrt{2})}^{2004}$•($\sqrt{3}$-$\sqrt{2}$)2004]•($\sqrt{3}$-$\sqrt{2}$)
=[(3-2)2004]•($\sqrt{3}$-$\sqrt{2}$)
=$\sqrt{3}$-$\sqrt{2}$
点评 本题考查了二次根式的混合运算、平方差公式的运用;熟练掌握平方差公式是解决问题的关键.

练习册系列答案
相关题目
19.有两根长度分别为15cm和25cm的小木棒,在下列长度的小木棒中选取一根,使之能与已有的两根搭成一个直角三角形,那么应该选取( )
| A. | 40cm | B. | 30cm | C. | 20cm | D. | 17cm |
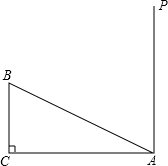 如图,有一个Rt△ABC,∠C=90°,AC=16,BC=8,一条线段MN=AB,M、N分别在AC和过点A且垂直于AC的射线AP上运动,问:点M运动到什么位置,才能使△ABC和△ANM全等.
如图,有一个Rt△ABC,∠C=90°,AC=16,BC=8,一条线段MN=AB,M、N分别在AC和过点A且垂直于AC的射线AP上运动,问:点M运动到什么位置,才能使△ABC和△ANM全等.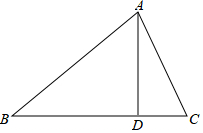 如图,D为△ABC边BC上的一点,AB=20,AC=13,AD=12,DC=5,则S△ABC=126.
如图,D为△ABC边BC上的一点,AB=20,AC=13,AD=12,DC=5,则S△ABC=126.