题目内容
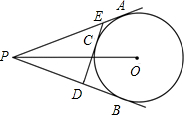如图，PA、PB、DE分别切⊙O于点A、B、C，⊙O的半径为6，OP=10．求△PDE的周长．考点：切线的性质,勾股定理,切线长定理
专题：
分析：如图，作辅助线，首先证明PA=PB=8；进而证明DE=EA+DB，问题即可解决．
解答：
解：连接OA；
∵PA、PB是⊙O的切线，
∴OA⊥PA，PA=PB=10；
由勾股定理得：PA2=PO2-OA2=100-36=64，
∴PA=PB=8；
∵EA、EC、DC、DB均为⊙O的切线，
∴EA=EC，DB=DC，
∴DE=EA+DB，
∴PE+PD+DE=PA+PB=16，
即△PDE的周长为16．
解：连接OA；∵PA、PB是⊙O的切线，
∴OA⊥PA，PA=PB=10；
由勾股定理得：PA2=PO2-OA2=100-36=64，
∴PA=PB=8；
∵EA、EC、DC、DB均为⊙O的切线，
∴EA=EC，DB=DC，
∴DE=EA+DB，
∴PE+PD+DE=PA+PB=16，
即△PDE的周长为16．
点评：该命题主要考查了切线的性质、切线长定理、勾股定理等几何知识点的应用问题；解题的关键是作辅助线，灵活运用有关定理来分析、判断．
练习册系列答案
相关题目
下列计算正确的是（ ）
| A、0-（-6）=-6 | ||||
| B、+9+（-4）=13 | ||||
C、
| ||||
| D、（-36）÷（-4）=9 |
如图，已知在四边形中，AC⊥BD交于点O，E、F、G、H分别是四边上的中点，求证：四边形EFGH是矩形．
半圆⊙O上依次有四个点A、B、C、D，且∠AOB=∠COD，求证：四边形ABCD是等腰梯形．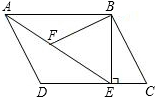
如图，在平行四边形ABCD中，AB=4，BC=3，过点B作BE⊥CD于E，连接AE，∠AEB=60°，F为AE上一点，且∠BFE=∠C．