题目内容
求函数y=-
x2+
x+2关于直线x=3对称的函数表达式.
| 1 |
| 2 |
| 3 |
| 2 |
考点:二次函数图象与几何变换
专题:几何变换
分析:把抛物线对称的问题转化为顶点对称的问题,利用配方法得到抛物线y=-
x2+
x+2的顶点坐标为(
,
),再确定点(
,
)关于直线x=3对称点的坐标为(
,
),然后根据顶点式写出对称后的抛物线解析式.
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
| 3 |
| 2 |
| 25 |
| 8 |
| 9 |
| 2 |
| 25 |
| 8 |
解答:解:∵y=-
x2+
x+2=-
(x-
)2+
,
∴抛物线y=-
x2+
x+2的顶点坐标为(
,
),
而点(
,
)关于直线x=3对称点的坐标为(
,
),
∴函数y=-
x2+
x+2关于直线x=3对称的函数表达式为y=-
(x-
)2+
=-
x2+
x+7.
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
∴抛物线y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
而点(
| 3 |
| 2 |
| 25 |
| 8 |
| 9 |
| 2 |
| 25 |
| 8 |
∴函数y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 25 |
| 8 |
| 1 |
| 2 |
| 9 |
| 2 |
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
3.14159…取精确到百分位的近似值是( )
| A、3.1 | B、3.14 |
| C、3.142 | D、3.1416 |
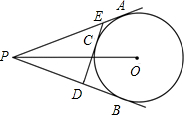 如图,PA、PB、DE分别切⊙O于点A、B、C,⊙O的半径为6,OP=10.求△PDE的周长.
如图,PA、PB、DE分别切⊙O于点A、B、C,⊙O的半径为6,OP=10.求△PDE的周长. 某城市12个月平均最高气温T(℃)与月份m的函数关系如图,求该城市1月,7月的平均最高气温.
某城市12个月平均最高气温T(℃)与月份m的函数关系如图,求该城市1月,7月的平均最高气温.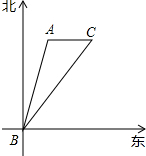 小明在课外实践活动中,在B处观测某建筑物A在北偏东15°方向,小明沿东北方向的公路BC以10km/h的速度前进,30min到达C处,测得A在正西方向,求建筑物A到BC的距离.
小明在课外实践活动中,在B处观测某建筑物A在北偏东15°方向,小明沿东北方向的公路BC以10km/h的速度前进,30min到达C处,测得A在正西方向,求建筑物A到BC的距离.