Question

1．如果菱形的两条对角线长分别为6和8，那么这个菱形一边上的高是$\frac{24}{5}$．

Answer 1

分析 根据对角线的长度即可计算菱形的面积，根据菱形对角线互相垂直平分的性质，可以求得△AOB为直角三角形，根据AO，BO可以求得AB的值，根据菱形的面积和边长即可解题．

解答 解：由题意知AC=6，BD=8，则菱形的面积S=$\frac{1}{2}$×6×8=24，
∵菱形对角线互相垂直平分，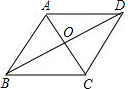
∴△AOB为直角三角形，AO=3，BO=4，
∴AB=$\sqrt{A{O}^{2}+B{O}^{\;}}$=5，
∴菱形的高h=$\frac{S}{AB}$=$\frac{24}{5}$．
故答案为：$\frac{24}{5}$．

点评 本题考查了勾股定理在直角三角形中的运用，菱形面积的计算，本题中求根据AO，BO的值求AB是解题的关键．