题目内容
15.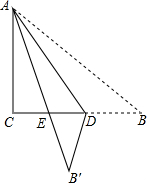 如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上运动,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若∠B′ED=90°,则BD的长是5.
如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上运动,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若∠B′ED=90°,则BD的长是5.
分析 设BD=x,由折叠得:B′D=x,CD=8-x,B′C=10-6=4,根据勾股定理列方程即可.
解答  解:当∠B′ED=90°时,如图所示,点C与E重合,
解:当∠B′ED=90°时,如图所示,点C与E重合,
设BD=x,则CD=8-x,
由折叠得:B′D=x,
∵∠ACB=90°,AC=6,BC=8,
∴AB=10,
∴AB′=AB=10,
∴B′C=10-6=4,
在Rt△CDB′中,B′D2=B′C2+CD2,
则x2=42+(8-x)2,
解得x=5,
∴BD=5,
故答案为:5.
点评 本题考查了等腰直角三角形和折叠问题,明确折叠的性质:折叠前后的边和角对应相等,本题是常考题型,难度不大,与方程相结合,利用勾股定理解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 如图,在比例尺为1:150 000的某城市地图上,若量得A、B两所学校的距离是4.2cm,则A、B两所学校的实际距离是( )
如图,在比例尺为1:150 000的某城市地图上,若量得A、B两所学校的距离是4.2cm,则A、B两所学校的实际距离是( )
 如图,在比例尺为1:150 000的某城市地图上,若量得A、B两所学校的距离是4.2cm,则A、B两所学校的实际距离是( )
如图,在比例尺为1:150 000的某城市地图上,若量得A、B两所学校的距离是4.2cm,则A、B两所学校的实际距离是( )| A. | 630米 | B. | 6300米 | C. | 8400米 | D. | 4200米 |
9.已知整式x2+x+2的值是6,那么整式4x2+4x-6的值是( )
| A. | 10 | B. | 16 | C. | 18 | D. | -12 |
5.已知二次函数y=x2-2mx+m2+3(m是常数),把该函数的图象沿y轴平移后,得到的函数图象与x轴只有一个公共点,则应把该函数的图象( )
| A. | 向上平移3个单位 | B. | 向下平移3个单位 | C. | 向上平移1个单位 | D. | 向下平移1个单位 |
11. 如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=120cm2,DE长是( )
如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=120cm2,DE长是( )
 如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=120cm2,DE长是( )
如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=120cm2,DE长是( )| A. | 4cm | B. | 4.8cm | C. | 5cm | D. | 无法确定 |
4.等腰△ABC的两边长分别是2和5,则△ABC的周长是( )
| A. | 9 | B. | 9或12 | C. | 12 | D. | 7或12 |
5.电脑病毒传播快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.若每轮感染中平均一台电脑会感染x台电脑,则下面所列方程中正确的是( )
| A. | x(x+1)=81 | B. | 1+x+x2=81 | C. | (1+x)2=81 | D. | 1+(1+x)2=81 |
 ,电子表上实际显示的时间为16:25:08.
,电子表上实际显示的时间为16:25:08.