题目内容
5.已知二次函数y=x2-2mx+m2+3(m是常数),把该函数的图象沿y轴平移后,得到的函数图象与x轴只有一个公共点,则应把该函数的图象( )| A. | 向上平移3个单位 | B. | 向下平移3个单位 | C. | 向上平移1个单位 | D. | 向下平移1个单位 |
分析 先化成顶点式,根据顶点坐标和平移的性质得出即可.
解答 解:y=x2-2mx+m2+3=(x-m)2+3,
把函数y=(x-m)2+3的图象沿y轴向下平移3个单位长度后,得到函数y=(x-m)2的图象,它的顶点坐标是(m,0),
因此,这个函数的图象与x轴只有一个公共点,
所以,把函数y=x2-2mx+m2+3的图象沿y轴向下平移3个单位长度后,得到的函数的图象与x轴只有一个公共点.
故选B.
点评 本题考查了二次函数和x轴的交点问题,利用平移的性质,二次函数的图象与几何变换的应用是解答此题的关键.

练习册系列答案
相关题目
16.某旅游景点8月份共接待游客25万人次,10月份共接待游客64万人次.设每月的平均增长率为x,则可列方程为( )
| A. | 25(1+x)2=64 | B. | 25(1-x)2=64 | C. | 64(1+x)2=25 | D. | 64(1-x)2=25 |
14.下列命题:
①一腰和底边对应相等的两个等腰三角形全等;
②腰长相等,且都有一个40°角的两个等腰三角形全等;
③腰长相等,且都有一个100°角的两个等腰三角形全等;
④腰和定焦对应相等的两个等腰三角形全等;
⑤两个等边三角形全等;
其中正确的命题的个数有( )
①一腰和底边对应相等的两个等腰三角形全等;
②腰长相等,且都有一个40°角的两个等腰三角形全等;
③腰长相等,且都有一个100°角的两个等腰三角形全等;
④腰和定焦对应相等的两个等腰三角形全等;
⑤两个等边三角形全等;
其中正确的命题的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
20.已知点A(a,b)与点B(2,2)是关于原点O的对称点,则( )
| A. | a=-2,b=-2 | B. | a=-2,b=2 | C. | a=2,b=-2 | D. | a=2,b=2 |
9.已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
| A. | a:b:c=4:5:6 | B. | b 2=a2-c2 | C. | ∠A=∠C-∠B | D. | a=3,b=4,c=5 |
12.下列命题中,是假命题的是( )
| A. | 互补的两个角不能都是锐角 | B. | 所有的直角都相等 | ||
| C. | 乘积是1的两个数互为倒数 | D. | 若a⊥b,a⊥c,则b⊥c |
13. 如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )
如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )
 如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )
如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
 如图,AB是圆O的直径,弧$\widehat{BC}$=弧$\widehat{CD}$=弧$\widehat{DE}$,∠COD=48°,则∠AOE的度数为36°.
如图,AB是圆O的直径,弧$\widehat{BC}$=弧$\widehat{CD}$=弧$\widehat{DE}$,∠COD=48°,则∠AOE的度数为36°.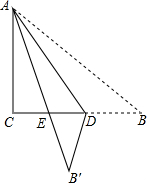 如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上运动,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若∠B′ED=90°,则BD的长是5.
如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上运动,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若∠B′ED=90°,则BD的长是5.