题目内容
4.等腰△ABC的两边长分别是2和5,则△ABC的周长是( )| A. | 9 | B. | 9或12 | C. | 12 | D. | 7或12 |
分析 分为两种情况:①当腰是2时,②当腰是5时,看看三角形的三边是否符合三角形的三边关系定理,求出即可.
解答 解:分为两种情况:①当腰是2时,三边为2,2,5,
∵2+2<5,
∴不符合三角形三边关系定理,此种情况不可能;
②当腰是5时,三边为2,5,5,
此时符合三角形三边关系定理,三角形的周长是2+5+5=12;
故选C.
点评 本题考查了等腰三角形的性质和三角形三边关系定理的应用,注意要进行分类讨论.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
12.下列命题中,是假命题的是( )
| A. | 互补的两个角不能都是锐角 | B. | 所有的直角都相等 | ||
| C. | 乘积是1的两个数互为倒数 | D. | 若a⊥b,a⊥c,则b⊥c |
9.二次函数y=(x-2)2+5的对称轴是( )
| A. | x=-2 | B. | x=2 | C. | x=-5 | D. | x=5 |
16.下列各组数中,互为相反数的是 ( )
| A. | -2与$\root{3}{-8}$ | B. | -2与-$\sqrt{4}$ | C. | -2与-$\frac{1}{2}$ | D. | -2与$\root{3}{8}$ |
13. 如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )
如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )
 如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )
如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
12.化简(2+1)(22+1)(24+1)(28+1)得( )
| A. | 28-1 | B. | 216+1 | C. | 216-1 | D. | 264-1 |
 如图,AB是圆O的直径,弧$\widehat{BC}$=弧$\widehat{CD}$=弧$\widehat{DE}$,∠COD=48°,则∠AOE的度数为36°.
如图,AB是圆O的直径,弧$\widehat{BC}$=弧$\widehat{CD}$=弧$\widehat{DE}$,∠COD=48°,则∠AOE的度数为36°.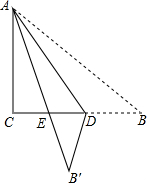 如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上运动,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若∠B′ED=90°,则BD的长是5.
如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上运动,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若∠B′ED=90°,则BD的长是5.