题目内容
11. 如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=120cm2,DE长是( )
如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=120cm2,DE长是( )| A. | 4cm | B. | 4.8cm | C. | 5cm | D. | 无法确定 |
分析 过点D作DF⊥BC交BC的延长线于F,根据角平分线上的点到角的两边距离相等可得DF=DE,然后根据△ABC的面积列出方程求解即可.
解答  解:如图,过点D作DF⊥BC交BC的延长线于F,
解:如图,过点D作DF⊥BC交BC的延长线于F,
∵BD是∠ABC平分线,DE⊥AB,
∴DF=DE,
∵S△ABC=120cm2,
∴$\frac{1}{2}$AB•DE+$\frac{1}{2}$BC•DF=120,
即$\frac{1}{2}$×36•DE+$\frac{1}{2}$×24•DE=120,
解得DE=4cm.
故选A.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并根据三角形的面积列出方程是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.用四舍五入法把3.8963精确到百分位得到的近似数是( )
| A. | 3.896 | B. | 3.900 | C. | 3.9 | D. | 3.90 |
20.已知点A(a,b)与点B(2,2)是关于原点O的对称点,则( )
| A. | a=-2,b=-2 | B. | a=-2,b=2 | C. | a=2,b=-2 | D. | a=2,b=2 |
20.若(x+y)2=11,(x-y)2=7,则xy和(x2+y2)的值分别为( )
| A. | 4,18 | B. | 1,18 | C. | 1,9 | D. | 4,9 |
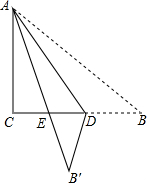 如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上运动,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若∠B′ED=90°,则BD的长是5.
如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上运动,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若∠B′ED=90°,则BD的长是5.