题目内容
19.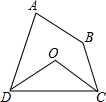 如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是( )
如图,四边形ABCD中,∠A+∠B=200°,∠ADC、∠DCB的平分线相交于点O,则∠COD的度数是( )| A. | 110° | B. | 100° | C. | 90° | D. | 80° |
分析 由于∠A+∠B=200°,根据四边形的内角和定理求出∠ADC+∠DCB的度数,然后根据角平分线的定义得出∠ODC+∠OCD的度数,最后根据三角形内角和定理求出∠COD的度数.
解答 解:∵∠A+∠B+∠ADC+∠DCB=360°,∠A+∠B=200°,
∴∠ADC+∠DCB=160°.
又∵∠ADC、∠DCB的平分线相交于点O,
∴∠ODC=$\frac{1}{2}$∠ADC,∠OCD=$\frac{1}{2}$,
∴∠ODC+∠OCD=80°,
∴∠COD=180°-(∠ODC+∠OCD)=100°.
故选B.
点评 本题主要考查了三角形及四边形的内角和定理.三角形的内角和等于180°,四边形的内角和等于360°

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
4.在△ABC中,∠A+∠B=120°,∠C=∠A,则△ABC是( )
| A. | 钝角三角形 | B. | 等腰直角三角形 | C. | 直角三角形 | D. | 等边三角形 |
9.在-2,0,2,$\sqrt{3}$这四个数中,最大的数是( )
| A. | -2 | B. | 2 | C. | $\sqrt{3}$ | D. | 0 |
 如图,已知⊙O1与⊙O2相交于点A、B,过点B作CD⊥AB,分别交⊙O1和⊙O2于点C、D,过点B任作一条直线分别交⊙O1和⊙O2于点E、F.求证:
如图,已知⊙O1与⊙O2相交于点A、B,过点B作CD⊥AB,分别交⊙O1和⊙O2于点C、D,过点B任作一条直线分别交⊙O1和⊙O2于点E、F.求证: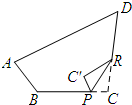 如图,将四边形纸片ABCD的右下角向内折出△PC′R,其中∠B=120°,∠D=40°,恰使C′P∥AB,RC′∥AD,则∠C=100°.
如图,将四边形纸片ABCD的右下角向内折出△PC′R,其中∠B=120°,∠D=40°,恰使C′P∥AB,RC′∥AD,则∠C=100°.