题目内容
 如图,∠AOB=30°,P点在∠AOB内部,M点在射线OA上,将线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点(OM>ON),若PM=
如图,∠AOB=30°,P点在∠AOB内部,M点在射线OA上,将线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点(OM>ON),若PM=| 10 |
考点:旋转的性质
专题:计算题
分析:连结MN,作NH⊥OA于H,如图,根据旋转的性质得∠MPN=90°,PN=PM=
,可判断△PMN为等腰直角三角形,则MN=
PM=2
,在Rt△OHN中,根据含30度的直角三角形三边的关系得NH=
ON=4,OH=
NH=4
,然后在Rt△MNH中根据勾股定理计算出MH=2,由此得到OM=OH+HM=4
+2.
| 10 |
| 2 |
| 5 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
解答:解:连结MN,作NH⊥OA于H,如图,
∵线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点,
∴∠MPN=90°,PN=PM=
,
∴△PMN为等腰直角三角形,
∴MN=
PM=2
,
在Rt△OHN中,∵∠NOH=30°,ON=8,
∴NH=
ON=4,
OH=
NH=4
,
在Rt△MNH中,∵NH=4,MN=2
,
∴MH=
=2,
∴OM=OH+HM=4
+2.
故答案为4
+2.

∵线段PM绕P点逆时针旋转90°,M点恰好落在OB上的N点,
∴∠MPN=90°,PN=PM=
| 10 |
∴△PMN为等腰直角三角形,
∴MN=
| 2 |
| 5 |
在Rt△OHN中,∵∠NOH=30°,ON=8,
∴NH=
| 1 |
| 2 |
OH=
| 3 |
| 3 |
在Rt△MNH中,∵NH=4,MN=2
| 5 |
∴MH=
| MN2-NH2 |
∴OM=OH+HM=4
| 3 |
故答案为4
| 3 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质和含30度的直角三角形三边的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,△ABC中,∠ACB=90°,CD⊥AB于D,BD=2,AD=8,求S△ABC.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,BD=2,AD=8,求S△ABC. 如图,在梯形ABCD中,AD∥BC,E、F分别是腰AB、DC的中点,四边形AEFD与四边形EBCF相似吗?为什么?
如图,在梯形ABCD中,AD∥BC,E、F分别是腰AB、DC的中点,四边形AEFD与四边形EBCF相似吗?为什么? “宝塔”是黄州城的古迹之一,有人想在塔外测量它的底角∠ABC的度数,如图,请问该如何测量?
“宝塔”是黄州城的古迹之一,有人想在塔外测量它的底角∠ABC的度数,如图,请问该如何测量?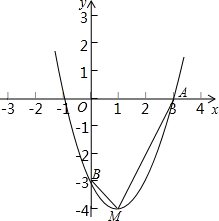 如图在直角坐标平面内,O为原点,点B坐标为(0,-3),且AO=BO,二次函数y=x2+bx+c经过A,B两点,顶点为M.
如图在直角坐标平面内,O为原点,点B坐标为(0,-3),且AO=BO,二次函数y=x2+bx+c经过A,B两点,顶点为M. 如图,有一块长为6.5单位长度,宽为2单位长度的长方形纸片,请把它分成6块,再拼成一个正方形,先在图中画出分割线,再画出拼后的图形,并标出相应的数据.
如图,有一块长为6.5单位长度,宽为2单位长度的长方形纸片,请把它分成6块,再拼成一个正方形,先在图中画出分割线,再画出拼后的图形,并标出相应的数据.