题目内容
11.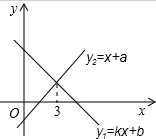 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0:③b>0;④x<2时,kx+b<x+a中,正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0:③b>0;④x<2时,kx+b<x+a中,正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据一次函数的图象与系数的关系对①②③进行判断;观察函数图象,当x>3时,一次函数y1=kx+b的图象都在移次函数y2=x+a的图象的下方,则可对④进行判断.
解答 解:∵直线=kx+b过第一、二、四象限,
∴k<0,b>0,所以①③正确;
∵直线y2=x+a的图象与y轴的交点在x轴下方,
∴a<0,所以②错误;
当x>3时,kx+b<x+a,所以④错误.
故选B.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列运算中,正确的是( )
| A. | (2$\sqrt{3}$)2=6 | B. | $\sqrt{(-\frac{2}{5})^{2}}$=-$\frac{2}{5}$ | C. | $\sqrt{9+16}$=$\sqrt{9}$+$\sqrt{16}$ | D. | $\sqrt{(-9)×(-4)}$=$\sqrt{9}$×$\sqrt{4}$ |
16.△ABC的两条高的长度分别为4和12,若第三条高也为整数,则第三条高的长度是( )
| A. | 4 | B. | 4或5 | C. | 5或6 | D. | 6 |
3.化简$\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$的结果是( )
| A. | $\frac{a+b}{a-b}$ | B. | $\frac{b}{a-b}$ | C. | $\frac{a}{a+b}$ | D. | $\frac{b}{a+b}$ |
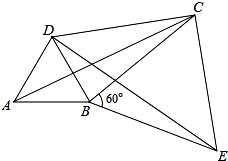 给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形. 一个圆柱被裁成几部分,如图是其中一个部分,求它的侧面积(可以试着剪一剪,看看它的侧面展开图)
一个圆柱被裁成几部分,如图是其中一个部分,求它的侧面积(可以试着剪一剪,看看它的侧面展开图) 已知数a与数b所表示的点在数轴上如图所示,则|a+b|-a=b.
已知数a与数b所表示的点在数轴上如图所示,则|a+b|-a=b.