题目内容
19.小王每天从某报社以每份0.6元买进报纸300份,然后以每份1元卖给读者,报纸卖不完,当天可退回报社,但报社只按每份0.3元退给小王,如果小王平均每天卖出报纸x份,纯收入为y元.(1)求y与x之间的函数关系式(要求写出自变量x的取值范围);
(2)如果每月以30天计算,小王每天至少要卖多少份报纸(假设小王每天所卖报纸份数相同)才能保证每月收入不低于2600元?
分析 (1)因为小王每天从某报社以每份0.6元买出报纸300份,然后以每份01元卖给读者,报纸卖不完,当天可退回报社,但报社只按每份0.3元退给小王,所以如果小王平均每天卖出报纸x份,纯收入为y元,则y=x+0.3(300-x)-0.6×300即y=0.7x-90,其中0≤x≤300且x为整数;
(2)因为每月以30天计,根据题意可得30(0.7x-90)≥2600,解之即可求解.
解答 解:(1)依题意得
y=x+0.3(300-x)-0.6×300=0.7x-90(0≤x≤300且x为整数);
(2)依题意:(0.7x-90)×30≥2600
解得:x≥252$\frac{8}{21}$
∴应取x≥253
∴小王每天至少要卖253份报纸才能保证每月收入不低于2600元.
点评 本题考查的是一次函数的应用以及一元一次不等式的应用,正确理解分析题意,正确列出函数关系式,利用不等式解决问题是本题的关键.

练习册系列答案
相关题目
9.在平面直角坐标系中,点A(5,-4)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.计算:1252-50×125+252=( )
| A. | 100 | B. | 150 | C. | 10000 | D. | 22500 |
8. 如图,要使?ABCD成为菱形,则需添加的一个条件是( )
如图,要使?ABCD成为菱形,则需添加的一个条件是( )
 如图,要使?ABCD成为菱形,则需添加的一个条件是( )
如图,要使?ABCD成为菱形,则需添加的一个条件是( )| A. | AC=AD | B. | BA=BC | C. | ∠ABC=90° | D. | AC=BD |
9.若(ax2-2xy+y2)-(-ax2+bxy+2y2)=6x2-9xy+cy2成立,则a,b,c的值分别为( )
| A. | 3,-7,-1 | B. | -3,7,-1 | C. | 3,7,-1 | D. | -3,-7,1 |
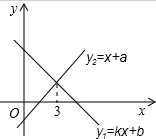 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0:③b>0;④x<2时,kx+b<x+a中,正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0:③b>0;④x<2时,kx+b<x+a中,正确的个数是( )