题目内容
2.已知$\left\{\begin{array}{l}{x=4}\\{y=-2}\end{array}\right.$与$\left\{\begin{array}{l}{x=-2}\\{y=-5}\end{array}\right.$都是方程y=kx+b的解.(1)求k,b的值;
(2)若y的值不小于0,求x的取值范围;
(3)若-2≤x<4,求y的取值范围.
分析 (1)把$\left\{\begin{array}{l}{x=4}\\{y=-2}\end{array}\right.$与$\left\{\begin{array}{l}{x=-2}\\{y=-5}\end{array}\right.$代入方程y=kx+b解答即可;
(2)根据方程变形列出不等式解答即可;
(3)根据方程变形列出不等式组解答即可.
解答 解:(1)由题意可得:$\left\{\begin{array}{l}{4k+b=-2}\\{-2k+b=-5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-4}\end{array}\right.$,
(2)由(1)得:y=$\frac{1}{2}x-4$,
因为y≥0,
可得:$\frac{1}{2}x-4≥0$,
解得:x≥8;
(2)由(1)得:y=$\frac{1}{2}x$-4,
可得:x=2y+8,
因为-2≤x<4,
所以可得:$\left\{\begin{array}{l}{2y+8≥-2}\\{2y+8<4}\end{array}\right.$,
解得:-5≤y<-2.
点评 此题考查了一元一次不等式的整数解,要熟练掌握,解答此类问题的关键在于正确解得不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式的整数解.可以借助数轴进行数形结合,得到需要的值,进而非常容易的解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.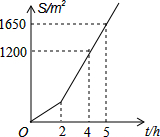 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )| A. | 300m2 | B. | 150m2 | C. | 330m2 | D. | 450m2 |
11.中国的领水面积约为370000km2,其中南海的领水面积约占我国领水面积的$\frac{1}{2}$,用科学记数法表示中国南海的领水面积是( )
| A. | 37×105km2 | B. | 37×104km2 | C. | 0.85×105km2 | D. | 1.85×105km2 |
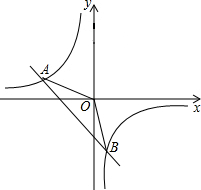 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).