题目内容
15.解下列方程(组)(1)$\frac{1}{x-2}$+3=$\frac{1-x}{2-x}$
(2)$\left\{\begin{array}{l}{3(x-5)=3y-6}\\{\frac{x-y}{3}=\frac{x+2y}{6}-2}\end{array}\right.$.
分析 (1)根据等式的性质,可得整式方程,根据解整式方程,可得方程的解;
(2)根据等式的性质,可化简方程组,根据加减消元法,可得方程组的解.
解答 解:(1)方程两边都乘以(x-2),得
1+3(x-2)=x-1.解得x=2,
检验:把x=2代入(x-2)=0,
∴x=2不是分式方程的解,
原分式方程无解;
(2)方程组化简,得$\left\{\begin{array}{l}{x-y=3①}\\{x-4y=-12②}\end{array}\right.$,
①-②,得
3y=15,
解得y=5,
把y=5代入①,得
x-5=-3,
解得x=2
原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$.
点评 本题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解,解分式方程一定注意要验根.

练习册系列答案
相关题目
5.下列实数中,是无理数的是( )
| A. | $\frac{22}{7}$ | B. | 2-2 | C. | $5.\stackrel{•}1\stackrel{•}5$ | D. | cos45° |
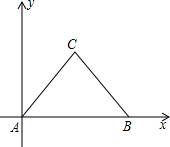 如图,等边△ABC中,点A为坐标原点,点B的坐标为(6,0),则点C的坐标为(3,3$\sqrt{3}$)或(3,-3$\sqrt{3}$).
如图,等边△ABC中,点A为坐标原点,点B的坐标为(6,0),则点C的坐标为(3,3$\sqrt{3}$)或(3,-3$\sqrt{3}$). 如图,直线AB、CD交于点O,OE⊥AB,若∠EOD=48°,则∠AOC=42°.
如图,直线AB、CD交于点O,OE⊥AB,若∠EOD=48°,则∠AOC=42°.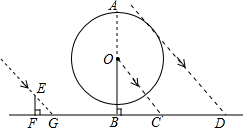 同一时刻甲、乙两组同学在阳光下进行测量,甲组将一根长为2.4m的竹竿EF直立于平地,测得竹竿的影长FG为1.8m;摩天轮的立柱OB直立于平地,乙组测得立柱OB的影长BC为36m,摩天轮在立柱右侧影子的边缘D与立柱OB相距86m,求摩天轮的半径和最高点A的高.
同一时刻甲、乙两组同学在阳光下进行测量,甲组将一根长为2.4m的竹竿EF直立于平地,测得竹竿的影长FG为1.8m;摩天轮的立柱OB直立于平地,乙组测得立柱OB的影长BC为36m,摩天轮在立柱右侧影子的边缘D与立柱OB相距86m,求摩天轮的半径和最高点A的高.