Question

Rt△ABC中，∠C=90°，AC=3，BC=4，把它分别沿三边所在直线旋转一周，求所得的三个几何体的全面积．

Answer 1

考点：圆锥的计算,点、线、面、体

专题：

分析：沿直角边所在直线旋转一周，得到圆锥，根据圆锥的全面积=侧面积+底面积即可求解；沿斜边所在直线旋转一周，得几何体为两个圆锥底面重合的组合体，那么全面积=两个圆锥的侧面积之和．

解答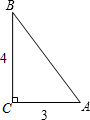：解：∵把Rt△ABC绕边AC所在直线旋转一周，
∴所得的几何体的全面积为：底面半径为4，母线长为5的圆锥侧面和半径为4的圆的面积之和，
故π×4×5+π×4²=36π．
∵把Rt△ABC绕边BC所在直线旋转一周，
∴所得的几何体的全面积为：底面半径为3，母线长为5的圆锥侧面和半径为3的圆的面积之和，
故π×3×5+π×3²=24π．
∵在Rt△ABC中，∠C=90°，AC=3，BC=4，
∴AB=

32+42

=5，
∴圆锥的底面半径=3×4÷5=2.4，
∵把Rt△ABC绕边AB所在直线旋转一周，
∴所得的几何体的全面积为：底面半径为2.4，母线长分别为4、3的两个圆锥侧面积之和，
∴圆锥的全面积=π×2.4×4+π×2.4×3=16.8π．

点评：此题主要考查了圆锥的侧面积公式、圆的面积公式和勾股定理的应用，根据已知得出几何体的组成部分是解题关键．