Question

19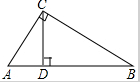．如图，在△ABC中，∠C=90°，CD⊥AB，AC=6，CD=5，求sinB．

Answer 1

分析 先利用等角的余角相等得到∠ACD=∠B，再在Rt△ACD中利用勾股定理计算出AD=$\sqrt{11}$，然后根据正弦的定义求解．

解答 解：∵CD⊥AB，
∴∠ADC=90°，
∴∠A+∠ACD=90°，
∵∠A+∠B=90°，
∴∠ACD=∠B，
在Rt△ACD中，∵AC=6，CD=5，
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{11}$，
∴sin∠ACD=$\frac{AD}{AC}$=$\frac{\sqrt{11}}{6}$，
∴sinB=$\frac{\sqrt{11}}{6}$．

点评 本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．解直角三角形要用到的关系：锐角互余的关系、三边之间的关系、边角之间的关系．