题目内容
9.点A的坐标为(1,3),点B的坐标为(2,0),试在y轴上找一点D,使点D到点A、B的距离最短并求出点D的坐标.分析 先画出直角坐标系,标出A、B点的坐标,再求出B点关于y轴的对称点C,连接AC,交y轴于点D,则D即为所求点,用待定系数法求出过AC两点的直线解析式,求出此解析式与y轴的交点坐标即可.
解答  解:作点B关于y轴的对称点C,连接AC,
解:作点B关于y轴的对称点C,连接AC,
∵B的坐标为(2,0),
∴C的坐标为(-2,0),
设过AC的直线解析式为y=kx+b(k≠0),
则$\left\{\begin{array}{l}{-2k+b=0}\\{k+b=3}\end{array}\right.$,
解得k=1,b=2,
故此直线的解析式为:y=x+2,
当x=0时,y=2,
即点D的坐标为(0,2).
点评 本题考查的是最短线路问题及用待定系数法求一次函数的解析式,熟知轴对称的性质及一次函数的相关知识是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知点P(4,-3),则P到x轴的距离为( )
| A. | 3 | B. | -3 | C. | 4 | D. | -4 |
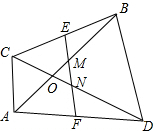 四边形ACBD中,AB、CD交于O,AB=CD,E、F是BC、AD的中点,判断△OMN的形状.
四边形ACBD中,AB、CD交于O,AB=CD,E、F是BC、AD的中点,判断△OMN的形状.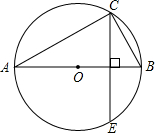 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,弦CE⊥AB于D,已知sinA=$\frac{3}{5}$,BC=4,则CE的长为$\frac{32}{5}$.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,弦CE⊥AB于D,已知sinA=$\frac{3}{5}$,BC=4,则CE的长为$\frac{32}{5}$.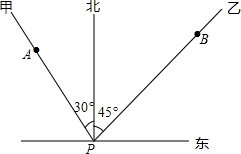 如图,点P表示某港口的位置,甲船在港口北偏西30°方向距港口50海里的A处,乙船在港口北偏东45°方向距港口60海里的B处,两船同时出发分别沿AP,BP方向匀速驶向港口P,1小时后乙船在甲船的正东方向处,已知甲船的速度是10海里/时,求乙船的速度.
如图,点P表示某港口的位置,甲船在港口北偏西30°方向距港口50海里的A处,乙船在港口北偏东45°方向距港口60海里的B处,两船同时出发分别沿AP,BP方向匀速驶向港口P,1小时后乙船在甲船的正东方向处,已知甲船的速度是10海里/时,求乙船的速度.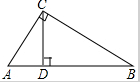 如图,在△ABC中,∠C=90°,CD⊥AB,AC=6,CD=5,求sinB.
如图,在△ABC中,∠C=90°,CD⊥AB,AC=6,CD=5,求sinB.